Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 16

Величина b_кр  для двухатомных газов, перегретого водяного пара, сухого насыщенного пара равна соответственно 0,528; 0,546 и 0,577. Для трехатомных газов b_кр  = 0,546, а для четырех и пятиатомных газов — 0,54.

Подставив значение b_кр  в уравнение (111.15), найдем, что значение максимальной скорости истечения, м/с:

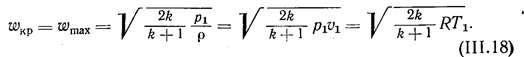
Видно, что значение максимальной скорости определяется физическими свойствами и начальными параметрами газа. При повышении скорости движения газа в соответствии с уравнением (111.8) будет происходить понижение его температуры. Поэтому еще до достижения максимальной скорости газ вначале потеряет свойства идеального газа, а затем, конденсируясь, будет превращаться в жидкость. Поэтому значение w_max представляет собой тот верхний теоретический предел скорости, к которому можно приблизиться, нагревая газы до высокой начальной температуры. Умножая уравнение (111.8) на kR, получим, что

Из физики известно, что kRТ* представляет собой квадрат скорости звука (a) в неподвижном газе, а c_р/R = k/(k-1), тогда получим, что

Следовательно, при адиабатном течении газа левая часть уравнения (III. 19) представляет собой квадрат скорости звука в неподвижном газе. Поэтому увеличение скорости движения газа будет сопровождаться уменьшением скорости звука в движущемся газе а.

Таким образом, максимальная (критическая) скорость истечения газа стремится к скорости распространения звука в неподвижном газе а*. Для идеального газа а*=(kRТ*)^1/2. Следует заметить, что k зависит от температуры, а R = 8314,2/m зависит от молекулярной массы газа. Поэтому скорость звука в водороде почти в 4 раза больше, чем в воздухе.

Критическому давлению в сопле соответствует и критическая температура потока, определяемая выражением

Максимальный секундный расход газа, кг/с, при критическом значении b_кр можно определить из уравнения (111.16), если в него подставить

Тогда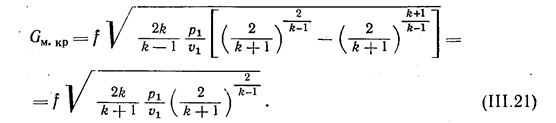

Он определяется начальными параметрами и природой идеального газа, а также площадью сечения канала.

В зависимости от отношения давлений b_кр = р₂/р₁ возможны два случая истечения газа. Здесь и далее под р₂ понимается давление окружающей среды p_окр. Если b > b_окр , то скорость истечения менее критической и расход газа менее максимального. В этом случае вся потенциальная энергия газа будет переведена в кинетическую. При b > b_окр скорость истечения и расход газа будут максимальными (рис. 11). При дальнейшем уменьшении давления р₂ величина b становится меньше критической, однако расход при этом не меняется оставаясь равным критическому.

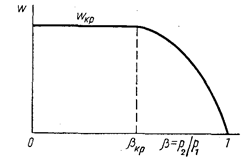Рис. 11. Изменение скорости истечения газа из сопла в зависимости от b

Это объясняется тем, что при давлении р₂ < p_кр в сопле устанавливается давление, равное критическому р_кр = b_кр р₁. Оно не меняется при уменьшении р₂. Постоянному давлению p_кр соответствует максимальная скорость истечения w_mах  и постоянный максимальный расход газа. Часть потенциальной энергии газа, соответствующая разности давлений (b_кр p₁ - p_окр) будет расходоваться на перемешивание газового потока с веществом окружающей среды.

5.4. Сопло Лаваля

При движении газа по каналам переменного сечения будет меняться скорость газового потока. В соответствии с уравнением (111.12) будет также изменяться и плотность газов, что потребует совместного рассмотрения уравнения неразрывности (111.1) и уравнения Д. Бернулли (111.9). Исключив из этих уравнений плотность, можно определить зависимость между скоростью газов и сечением канала.

Продифференцировав уравнение неразрывности, получим, что

Разделив уравнение на wr f, получим связь между относительными изменениями скорости и площади сечения канала, т. е.

После дифференцирования правой части уравнения (111.9) и умножения ее на w/w получим, что

Так как dp/dr = а², то умножая уравнение (111.22) на эту величину, можно записать, что а² df / f+ а² dw/w + dp/r = 0.

Вычитая из этого уравнения выражение (III.23), получим, что.

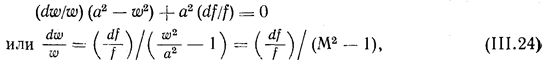
где М — отношение скорости потока к скорости звука, называемое числом Маха.