Теплофизика. Часть 1 «Основы термодинамики»: Учебное пособие, страница 28

Поэтому  можно  только  утверждать  что  энергия  подсистемы   (или  системы)   определяется  каким-т достаточно  узким  интервалом  между  Е  и  Е+ E ,  где  Е>>Е.  Кроме  того,   все  состояния   с  различной энергией   характеризуются   и    различными   вероятностями.    Если   нескольким    различным   состоянием системы  отвечает  одна  и  та  же  энергия,  то  такие  состояния  называются  в  ы  р  о  ж  д  е н  н ы  м и, а число состояний с одной и той же энергией  называют    к р а т н о с т ь ю   в ы р  о ж  д е  н и  я   или с т  а т и с т и ч е с к и м    в е с о м.                                                                                           

Величина  Е  достаточно    мала ,  поэтому   в  интервале  энергий  Е  +Е   все состояния   системы могут  быть  приняты  равновесными.  Пусть Q_m          -  вероятность  нахождения  системы   в  определенном  энергетическом состоянии.  Эта вероятность  равна отношению числа  возможных  состояний, при которых  система имеет энергию в интервале [E_m-(E_mE), к общему числу состояний системы  или

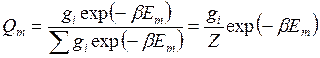                         (14.25)

где                                                          (14.26)

-с т ат и с т и ч а с к а я  с у м м а  термодинамической: системы, определяемая суммированием по энергетическим состояниям; Е ₁, Е₂ , ...,  Е_i   -  энергии, соответствующие  различным степеням свободы системы.                                                                              

В   общем   случае   энергия  атома  или   молекулы состоит из энергии  поступательного  движения Е и энергии внутренних степеней свободы Е :Е=Е  +  Е  ,  а статистическая сумма по состояниям имеет вид

    (14.27)

Статистическая сумма по состояниям энергии поступательного движения для газа объемом  V

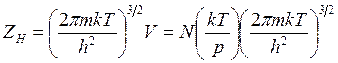      (14.28)    

Для определения статистической суммы по состояниям внутренней энергии необходимо знать, из чего складывается энергия внутренних степеней свободы. Пусть, например, система состоит из атомов н двухатомных молекул. У атомов энергии внутренних степеней свободы складывается из энергии возбужденных электронных состояний Е₀,Е₁,...,Е_m, соответствующих различным электронным конфигурациям. Статистическая сумма по возбужденным электронным состояниям в этом  случае будет иметь  вид                                                                       

                                                                                                         (14.29)

Для   многих  задач  можно ограничиться  только первым  членом соответствующим основному состоянию  E=0.  В этом случае                                                                     

   (14.30)    

Тогда для одноатомных газов                                                                   

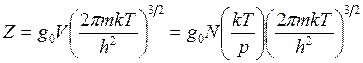                     (14.31)

Здесь  N - число атомов в системе; h  и  k- постоянные Планка и Больцмана;   m- относительная атомная масса.                                                                                 

В отличие от атомов, обладающих энергетическими состояниями только  одного типа, энергия внутренних степеней свободы двухатомных молекул складывается из энергии возбужденных  электронных состояний Е_i, энергии колебания ядер атомов относительно друг друга Е_k, энергии  вращения ядер относительно центра тяжести молекулы Е_вр .  В этом случае                                                                            

                      (14.32)

 где                 

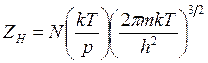
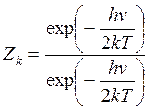
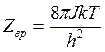 (14.33)

где  J - момент инерции молекулы;   - частота колебаний.                                       

Таким образом, для  вычисления статистической суммы по  состояниям любой  системы необходимо знать допустимые состояния и  уровни энергии.  При вычислении  этой суммы  каждое состояние рассчитывается  отдельно, поэтому  статистическая сумма  состояний  N  систем может  быть получена из параметров, определенных для одной молекулы путем возведения в степень N :