Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 9

Условие  в теореме является условием единственности.

Условие  является слишком ограничительным. Например, уравнение  этому условию не удовлетворяет на , т.к.  при .

Условие единственности  можно заменить более общим: единственность сохраняется, если 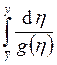 расходится (здесь ). При сходимости этого интеграла единственности может не быть.

Уравнение  при непрерывной функции  на  при любых начальных значениях  имеет единственное решение.

§1.3 Уравнения в полных дифференциалах. Интегрирующий множитель.

Рассмотрим уравнение . Предположим, что функции M и N определены, непрерывны, непрерывно дифференцируемы и одновременно не обращаются в ноль в некоторой области D. Тогда уравнение  – уравнение в полных дифференциалах, если .

Пусть . Тогда , т.е. . Таким образом, интегральные линии уравнения  оказываются линиями уровня функции .

Функция  называется первым интегралом уравнения .

Таким образом, общий интеграл уравнения можно получить, построив первый интеграл.

В случае односвязной области D уравнение  является уравнением в полных дифференциалах тогда и только тогда, когда .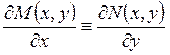

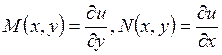Пусть уравнение  – уравнение в полных дифференциалах. Для построения  можно учесть, что  и восстановить . Можно также воспользоваться формулой 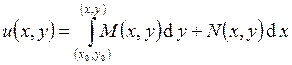. Здесь вычисляется криволинейный интеграл II-го рода по кривой, соединяющей точки  и . Точка  – фиксированная точка из D. Результат интегрирования не зависит от выбора пути интегрирования, т.к. подынтегральное выражение является полным дифференциалом некоторой функции, следовательно, пути интегрирования можно выбирать по своему усмотрению. Часто удобным оказывается составить его из участков, параллельным координатным осям.

Если 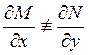, уравнение  не является уравнением в полных дифференциалах, однако его можно попытаться привести к такому с помощью интегрирующего множителя . Умножим  на  и потребуем, чтобы полученное уравнение было уравнением в полных дифференциалах, т.е. 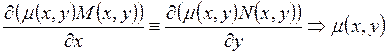 является решением уравнения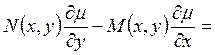 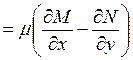 . Таким образом, выбирая функцию  среди решений этого уравнения и умножая на неё исходное уравнение, получаем уравнение в полных дифференциалах. Такая функция  называется интегрирующим множителем уравнения.

Заметим, что полученное уравнение является уравнением с частными производными I-го порядка. Решение такого уравнения в общем случае может оказаться более сложной задачей, чем решение исходного уравнения.

Нас интересует только одно решение этого уравнения и в некоторых случаях его можно подобрать.

§ 1.4 Линейные уравнения

Линейными уравнениями I-го порядка будем называть уравнения вида . Здесь  – коэффициент линейного уравнения,  – неоднородность линейного уравнения.

Если , то уравнение называется неоднородным, иначе – однородным. Если в уравнении формально отбросить , то получится соответствующее однородное уравнение.

Будем полагать, что функции  и  определены на . Зафиксируем точку . Дополним линейное уравнение начальным условием . В результате мы получили задачу Коши.

Пусть  и  непрерывны на . Тогда задача Коши имеет единственное решение, определённое на .

3.  Единственность: Пусть задача Коши имеет два различных решения  и . Тогда  удовлетворяет уравнению  и начальному условию . Имеем уравнение с разделяющимися переменными, 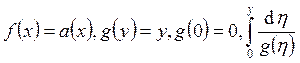 расходится, следовательно задача Коши имеет единственное решение  (см. второе замечание § 1.2), что противоречит условию.

4.  Существование: Пусть существует функция , являющаяся решением задачи Коши. Получим представление для неё: . Умножим обе части тождества на 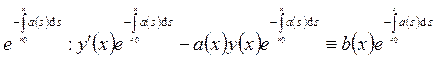. Преобразуем получившееся выражение: 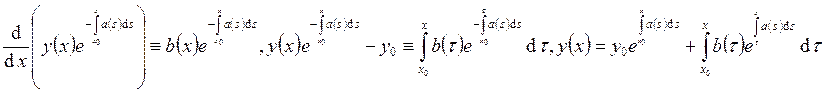. Таким образом, решение задачи Коши, если оно существует, представляется в виде этого тождества. Рассмотрим его. В правой части имеем непрерывно дифференцируемую функцию, определённую при . Подставив её в уравнение, проведя преобразования в обратном порядке, убедимся, что она – решение этого уравнения. Таким образом, решения задачи Коши существуют.

Линейное уравнение всегда имеет интегрирующий множитель .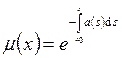

Способы решения линейных уравнений:

3.  Метод интегрирующего множителя.