Если хотя
бы в одной точке ![]() , то функции линейно независимы.
, то функции линейно независимы.
Теорема о линейно независимых
решениях: Пусть ![]() –
решения уравнения
–
решения уравнения ![]() . Тогда
. Тогда ![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() линейно зависимы.
линейно зависимы.
Система
линейно независимых решений ![]() называется
фундаментально системой решений (ФСР) этого уравнения. ФСР существует, т.к.
решения
называется
фундаментально системой решений (ФСР) этого уравнения. ФСР существует, т.к.
решения ![]() , обладающие свойством линейной независимости
можно построить так:
, обладающие свойством линейной независимости
можно построить так: 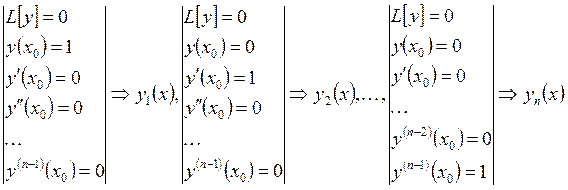 . При этом
. При этом 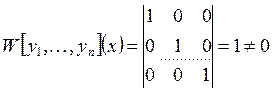 .
.
Теорема об общем решении
однородного линейного уравнения: Пусть ![]() – ФСР уравнения
– ФСР уравнения ![]() .
Тогда
.
Тогда ![]() – общее решение этого уравнения. Здесь
– общее решение этого уравнения. Здесь ![]() – произвольные постоянные.
– произвольные постоянные.
Система
решений ![]() уравнения
уравнения ![]() порядка
n линейно зависима.
порядка
n линейно зависима.
Множество
решений линейного уравнения ![]() образует линейное
пространство размерности n, причём ФСР – базис в этом пространстве.
образует линейное
пространство размерности n, причём ФСР – базис в этом пространстве.
Однородное линейное уравнение можно решить, построив ФСР. В общем случае уравнений с переменными коэффициентами общего метода построения ФСР нет. Возможно понижение порядка, если известно хотя бы одно нетривиальное решение уравнения. На этом пути в простейших случаях удаётся получить ФСР.
Уравнения с постоянными коэффициентами решаются всегда. ФСР однородного уравнения с постоянными коэффициентами всегда можно решить методом Эйлера.
§ 2.4 Решение однородных линейных уравнений с постоянными коэффициентами
Рассмотрим уравнение ![]() , предполагая, что
, предполагая, что ![]() постоянны.
Найдём ФСР. Воспользуемся для этого подстановкой Эйлера: будем искать решения
уравнения в виде
постоянны.
Найдём ФСР. Воспользуемся для этого подстановкой Эйлера: будем искать решения
уравнения в виде ![]() , где k
– постоянная. Подставляем
, где k
– постоянная. Подставляем ![]() в уравнение
в уравнение 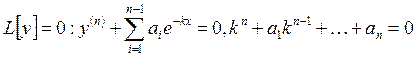 .
.
Это
уравнение называется характеристическим уравнением уравнения ![]() .
.
Это алгебраическое уравнение степени n с вещественными коэффициентами. По основной теореме алгебры такое уравнение всегда имеет ровно n корней в комплексных числах с учётом их кратности.
3. Характеристическое
уравнение имеет простые вещественные корни: ![]() при
при ![]() . По формуле
. По формуле ![]() получаем
решения:
получаем
решения: ![]() . Таких решений n
и они линейно независимы, т.к.
. Таких решений n
и они линейно независимы, т.к. 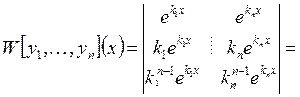 (определитель
Вандермонда)
(определитель
Вандермонда) 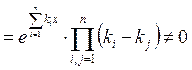 , следовательно,
, следовательно, ![]() образуют ФСР. Таким образом, общее решение
–
образуют ФСР. Таким образом, общее решение
– 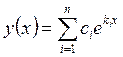 .
.
4. Характеристическое
уравнение имеет простые корни, среди которых есть комплексные: ![]() . Выбираем произвольно корень уравнения
. Выбираем произвольно корень уравнения ![]() . Если он вещественный, то по формуле
. Если он вещественный, то по формуле ![]() получаем вещественное решение, иначе –
получаем вещественное решение, иначе – ![]() . Т.к. характеристическое уравнение имеет
вещественные коэффициенты, то
. Т.к. характеристическое уравнение имеет
вещественные коэффициенты, то ![]() . Этим двум корням по
формуле
. Этим двум корням по
формуле ![]() ставим в соответствие комплексное решение:
ставим в соответствие комплексное решение:
![]() . Выбираем
. Выбираем ![]() (в
последнем случае знак – произвольно). Таким образом, каждому корню
характеристического уравнения сопоставляется вещественное решение уравнения
(в
последнем случае знак – произвольно). Таким образом, каждому корню
характеристического уравнения сопоставляется вещественное решение уравнения ![]() . Таких решений n.
Можно показать, что они линейно независимы, следовательно, они образуют ФСР,
откуда можно получить общее решение уравнения.
. Таких решений n.
Можно показать, что они линейно независимы, следовательно, они образуют ФСР,
откуда можно получить общее решение уравнения.
4. Характеристическое
уравнение имеет корни ![]() соответственной кратности
соответственной кратности ![]() . Заметим, что
. Заметим, что ![]() для
для ![]() . Будем сопоставлять каждому корню
. Будем сопоставлять каждому корню ![]() решений уравнения
решений уравнения ![]() .
Выбираем произвольно корень
.
Выбираем произвольно корень ![]() . Если
. Если ![]() , этот корень простой, следовательно, по
формуле
, этот корень простой, следовательно, по
формуле ![]() ему ставится в соответствие решение
ему ставится в соответствие решение ![]() (комплексное либо вещественное). Если
(комплексное либо вещественное). Если ![]() кратны, т.е.
кратны, т.е. ![]() , то эта
формула позволяет получить только одно решение, следовательно, имеются
недостающие решения. Однако легко показать, что решениями являются также
функции
, то эта
формула позволяет получить только одно решение, следовательно, имеются
недостающие решения. Однако легко показать, что решениями являются также
функции ![]() . В целом получается
. В целом получается ![]() решений, следовательно всего уравнению
решений, следовательно всего уравнению ![]() сопоставляют
сопоставляют ![]() решений.
Если корень
решений.
Если корень ![]() вещественный, то все приведённые решения
вещественны. Если
вещественный, то все приведённые решения
вещественны. Если ![]() – комплексный, то найдётся ещё
один корень
– комплексный, то найдётся ещё
один корень ![]() . Соответственно этим двум корням можно
сопоставить вещественное решение
. Соответственно этим двум корням можно
сопоставить вещественное решение 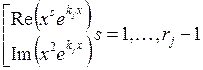 . В результате
получается n решений. Можно показать, что они
линейно независимы, следовательно, они образуют ФСР, откуда получается общее
решение.
. В результате
получается n решений. Можно показать, что они
линейно независимы, следовательно, они образуют ФСР, откуда получается общее
решение.
Некоторые
уравнения, изначально с переменными коэффициентами, приводятся к уравнениям с
постоянными коэффициентами с помощью замены переменных, в том числе уравнение
Эйлера: ![]() (
(![]() – постоянные). Это уравнение
приводится к уравнению с постоянными коэффициентами заменой
– постоянные). Это уравнение
приводится к уравнению с постоянными коэффициентами заменой ![]() . Отсюда следует, что уравнение Эйлера
можно решать и непосредственно, не приводя его к уравнению с постоянными
коэффициентами с помощью степенной подстановки Эйлера:
. Отсюда следует, что уравнение Эйлера
можно решать и непосредственно, не приводя его к уравнению с постоянными
коэффициентами с помощью степенной подстановки Эйлера: ![]() .
.
§2.5 Формула Остроградского-Лиувилля
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.