Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 15

Таким образом, задача переходит в задачу на собственные значения, или задачу Штурма-Лиувилля. Решить задачу на собственные значения значит найти все собственные значения и собственные функции этой задачи.

Свойства собственных значений и собственных функций:

1.  Собственные значения существуют и их счётное множество.

2.  Собственные значения вещественны.

3.  В случае  и  все собственные значения положительны.

4.  Ранг каждого собственного значения равен 1, т.е. любому собственному значению соответствует только одна линейно независимая собственная функция.

5.  Собственные функции, соответствующие различным собственным числам ортогональны с весом , т.е. , где  и  – собственные функции, соответствующие собственным значениям  (т.е.  – скалярное произведение ).

Теорема Стеклова: Любую непрерывную дважды дифференцируемую на  функцию , удовлетворяющую условиям 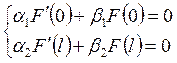 можно разложить в абсолютно и равномерно сходящийся ряд по собственным функциям краевой задачи:  (обобщённый ряд Фурье), где 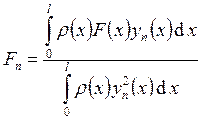 (коэффициенты Фурье).

Доказательство 4-го свойства: Предположим, что собственному значению  соответствуют линейно независимые  и . Тогда  и  – решение уравнения при  и, т.к. они линейно независимы, то они образуют ФСР, следовательно,  на . С другой стороны,  и  удовлетворяют краевым условиям. Рассмотрим условия при , . 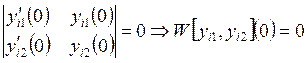Имеем систему уравнений относительно , которая имеет нетривиальное решение , следовательно, матрица этой системы вырожденная: , следовательно, двух линейно независимых функций быть не может.

Глава 4. Системы дифференциальных уравнений.

§4.1 Нормальные системы.

В общем случае систему дифференциальных уравнений можно представить в виде . Имеем систему k уравнений относительно m неизвестных.

Введём:  – порядок системы относительно неизвестной , а p  общий порядок системы.

Пусть система приводится к виду 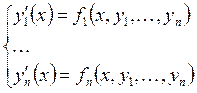. Эта система называется нормальной системой, порядок её равен n.

Предположим, что функции  определены в некоторой области . Фиксируем точку  и добавляем начальные условия: .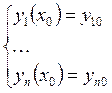

Пусть функции  непрерывны в D и непрерывно дифференцируемы по . Тогда найдётся такой отрезок  и , на котором задача Коши имеет единственное решение. Отметим, что решением системы называется совокупность функций , непрерывных и непрерывно дифференцируемых, которые, будучи подставленными в систему, превращают эту систему в систему тождеств.

При условиях теоремы общее решение системы имеет вид .

Геометрически решениям системы отвечает линия в пространстве переменных , называемая интегральной линией. Общему решению системы ставится в соответствие семейство интегральных линий. При условиях теоремы интегральные линии не пересекаются.

Пространство переменных  называется фазовым пространством системы. Проекция интегральной линии на фазовое пространство называется фазовой траекторией системы. При этом обычно указывается также и направление движения по фазовой траектории при возрастании аргумента x. В общем случае даже при условиях теоремы фазовые траектории могут пересекаться.

Система 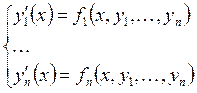 называется автономной, если в правой части  (не зависят явным образом от x).

Фазовые траектории автономной системы при условиях теоремы не пересекаются.

Совокупность фазовых траекторий системы называется фазовым портретом этой системы.

Системы уравнений вида 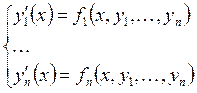 оказывается удобным записывать в векторной форме: 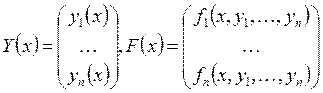. Тогда эта система приводится к виду . Здесь .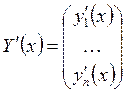

§1.2 Линейные системы. Общие свойства линейных систем.

Рассмотрим системы вида . Такие системы будем называть линейными. Здесь A – матрица системы (матрица коэффициентов системы). Если A – постоянна, то эта система называется системой с постоянными коэффициентами, иначе – системой с переменными коэффициентами. Векторная функция  – это неоднородность системы. Если , то система однородна, иначе – неоднородна.

Будем использовать обозначения: 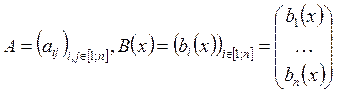. Будем полагать, что  и  определены на .

Дополним систему условием: , где  – фиксирована. Имеем задачу Коши. Пусть  и  непрерывны на . Тогда задача Коши имеет единственное решение на всём .