Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 14

В дальнейшем будем рассматривать вместо этого уравнения уравнение  на . Будем полагать, что функции  определены и непрерывны на  и  на .

Приведённые условия позволяют легко перейти от первого уравнения ко второму. Действительно, . Возможен и обратный переход: домножим первое уравнение на 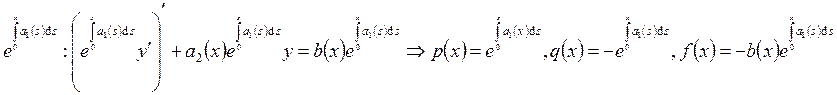. Отсюда следует, что вся предыдущая теория переносится на уравнения второго вида.

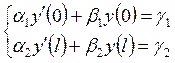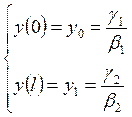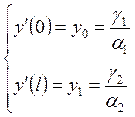Рассмотрим для этого уравнения краевые задачи, дополняя его краевыми условиями: . (эти краевые условия часто называют условиями Штурма-Лиувилля). Эти условия рассматриваются при естественных ограничениях: . Если в этих условиях , то они принимают вид:  и называются краевыми условиями I рода, а задача – I-й краевой задачей. Если , то условия принимают вид:  и называются краевыми условиями II рода, а задача – II краевой задачей. Если все коэффициенты отличны от 0, то эти условия называются условиями III рода, а задача – III краевой задачей. Если на концах промежутка  заданы условия разных типов, то задача называется смешанной краевой задачей. Если в уравнении  и , то задача называется однородной краевой задачей, иначе – неоднородной краевой задачей.

§ 3.2 Решение неоднородных краевых задач. Функция Грина.

Рассмотрим неоднородную краевую задачу: 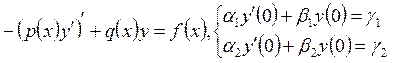, где ,  определены и непрерывны на  на . Далее будем полагать, что . В противном случае от этих неоднородностей можно избавиться соответствующей заменой переменных.

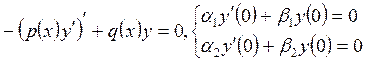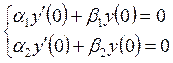Пусть однородная краевая задача –  имеет единственное решение . Тогда соответствующая неоднородная краевая задача – ,  – имеет единственное решение при любой неоднородности .

Рассмотрим однородное уравнение – . При наших условиях ФСР этого уравнения существует: , следовательно, можно написать общее решение: . Модифицируем ФСР, согласовав его с краевыми условиями. Пусть  – решение, удовлетворяющее первому из двух краевых условий (при ). Оно находится соответствующим выбором  и . Отметим, что , следовательно,  не удовлетворяет условию при . Аналогично  – решение, удовлетворяющее условию при  и не удовлетворяющее при и  линейно независимы по построению, следовательно, они образуют ФСР. Имеем общее решение: . Варьируем постоянные: . Найдём решение неоднородной задачи в виде 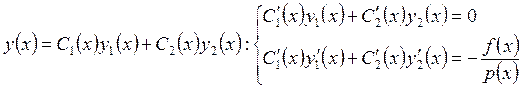. Отсюда  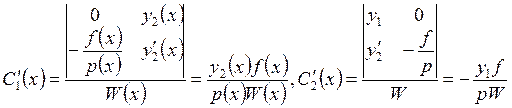(здесь  – определитель Вронского). 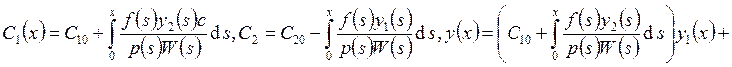 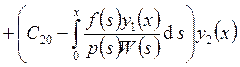. Удовлетворим краевые условия. При  получаем:   . 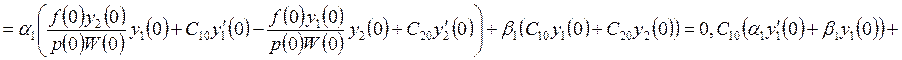При этом  по построению функции . Следовательно, это равенство будет выполняться при  и при . Рассмотрим условие при 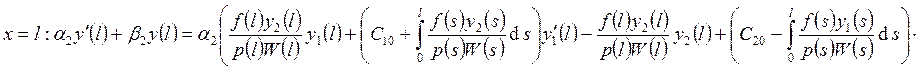  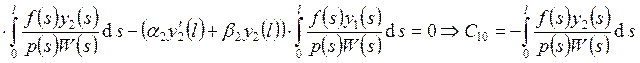 . Таким образом, решение краевой задачи есть 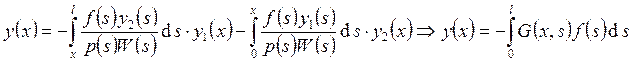, где 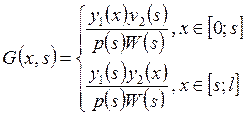. Таким образом, построено решение краевой задачи. Оно определяется формулой 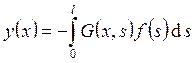. Построенное решение единственно. Предположив, что есть ещё одно решение, отличное от построенного, можно рассмотреть разность двух решений. Эта разность является решением однородной краевой задачи, которая имеет только тривиальное решение (по условию). Получаем противоречие.

Функция  называется формулой Грина нашей краевой задачи. Построив её, можно сразу выписать решение краевой задачи. Отметим, что  не зависит от выбора f.

Свойства функции Грина:

5.   непрерывна на .

6.  При  как функция x удовлетворяет однородному уравнению .

7.   как функция x удовлетворяет краевым условиям (в силу выбора ).

8.   на диагонали  имеет скачок величины .

.

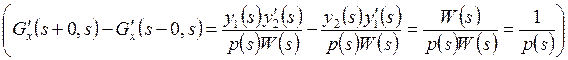Свойства 1-4 являются определяющими свойствами функции Грина: любая функция, обладающая этими свойствами является функцией Грина своей краевой задачи. Функция Грина определяется однозначно.

§3.3 Однородные краевые задачи. Собственные значения и собственные функции.

Рассмотрим однородную краевую задачу 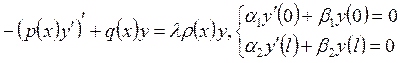. Здесь  определены и непрерывны на  и  – числовой параметр, . При любых значениях параметра l имеем однородную правую краевую задачу. У неё есть тривиальное решение . Интерес представляют нетривиальные решения этой задачи.

Значение параметра l, при котором краевая задача имеет нетривиальное решение называется собственным значением этой краевой задачи, а нетривиальные решения, соответствующие собственным значениям, называются собственными функциями этой краевой задачи.