3. Матрица A имеет собственные значения ![]() , т.е.
собственное значение является кратным. Тогда оно вещественное.
, т.е.
собственное значение является кратным. Тогда оно вещественное.
а) Собственному
значению l соответствует два
линейно независимых вектора ![]() и
и ![]() . Общее решение:
. Общее решение: 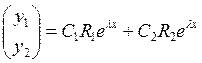 .
Все фазовые траектории прямолинейны. При
.
Все фазовые траектории прямолинейны. При ![]() точка покоя
точка покоя ![]() асимптотически
устойчива. Она называется устойчивым дикритическим узлом. При
асимптотически
устойчива. Она называется устойчивым дикритическим узлом. При ![]() точка покоя
точка покоя ![]() неустойчива.
Она называется неустойчивым дикритическим узлом.
неустойчива.
Она называется неустойчивым дикритическим узлом.
б)  Собственному
значению l соответствует один
линейно независимый вектор
Собственному
значению l соответствует один
линейно независимый вектор ![]() . Общее решение:
. Общее решение: 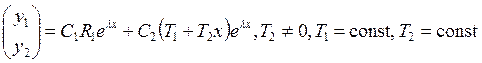 . Можно считать, что
. Можно считать, что ![]() . Здесь при
. Здесь при ![]() точка покоя
точка покоя ![]() асимптотически
устойчива. Она называется устойчивым (вырожденным) узлом. При
асимптотически
устойчива. Она называется устойчивым (вырожденным) узлом. При ![]() точка покоя
точка покоя ![]() неустойчива.
Она называется неустойчивым (вырожденным) узлом.
неустойчива.
Она называется неустойчивым (вырожденным) узлом.
Эта картина получается из первого
случая ![]() при
при ![]() .
.
Отметим, что из условия ![]() следует, что матрица A
не имеет нулевых собственных значений. Однако можно рассмотреть аналогичными
методами и случай вырожденной матрицы A.
следует, что матрица A
не имеет нулевых собственных значений. Однако можно рассмотреть аналогичными
методами и случай вырожденной матрицы A.
 Проведённый анализ позволяет
утверждать следующее:
Проведённый анализ позволяет
утверждать следующее:
1. Если все
собственные значения матрицы имеют отрицательную вещественную часть, то точка
покоя ![]() асимптотически устойчива (устойчивые узлы
и фокусы).
асимптотически устойчива (устойчивые узлы
и фокусы).
2. Если хотя
бы одно собственное значение матрицы имеет отрицательную вещественную часть, то
точка покоя ![]() неустойчива (неустойчивые узлы, сёдла).
неустойчива (неустойчивые узлы, сёдла).
Во втором случае второе собственное значение может быть нулевым. В остальных случаях требуется дополнительное условие.
Приведённые утверждения остаются справедливыми, если порядок системы равен n.
§5.3 Исследование на устойчивость по первому приближению
Рассмотрим
произвольную нелинейную систему ![]() . Предположим, что
. Предположим, что ![]() определена при
определена при ![]() . Пусть
для этой системы выполнены условия теоремы существования и единственности и
. Пусть
для этой системы выполнены условия теоремы существования и единственности и ![]() на
на ![]() .
Последнее условие обеспечивает существование точки покоя
.
Последнее условие обеспечивает существование точки покоя ![]() . Далее будем полагать, что функция
. Далее будем полагать, что функция ![]() в окрестности точки
в окрестности точки ![]() допускает разложение
допускает разложение ![]() , где
, где ![]() имеет
оценку:
имеет
оценку: ![]() , где M и g
– положительные постоянные. Сопоставим системе линейную систему
, где M и g
– положительные постоянные. Сопоставим системе линейную систему ![]() . Эта система называется системой первого
приближения, для первоначальной системы.
. Эта система называется системой первого
приближения, для первоначальной системы.
Система первого приближения называется стационарной, если матрица A постоянна.
Точка
покоя ![]() системы
системы ![]() является
также точкой покоя и системы первого приближения.
является
также точкой покоя и системы первого приближения.
Будем
говорить, что система ![]() допускает исследование точки
покоя
допускает исследование точки
покоя ![]() на устойчивость по первому приближению,
если эта точка является одновременно устойчивой (неустойчивой), как для системы
на устойчивость по первому приближению,
если эта точка является одновременно устойчивой (неустойчивой), как для системы
![]() , так и для системы
, так и для системы ![]() .
.
В
случае, когда система ![]() допускает исследование на
устойчивость по первому приближению, это исследование можно провести для более
удобной системы
допускает исследование на
устойчивость по первому приближению, это исследование можно провести для более
удобной системы ![]() .
.
Пусть ![]() допускает разложение
допускает разложение ![]() , где
, где ![]() имеет
оценку:
имеет
оценку: ![]() , где M и g
– положительные постоянные. Пусть при этом система первого приближения
, где M и g
– положительные постоянные. Пусть при этом система первого приближения ![]() стационарна. Тогда
стационарна. Тогда
1.
(теорема об устойчивости): Если
все собственные значения матрицы A имеют отрицательную вещественную часть, то исследование
на устойчивость по первому приближению точки покоя ![]() для
системы
для
системы ![]() возможно, причём точка покоя
возможно, причём точка покоя ![]() асимптотически устойчива.
асимптотически устойчива.
2.
(теорема о неустойчивости): Если
хотя бы одно собственное значение имеет положительную вещественную часть, то
исследование на неустойчивость по первому приближению точки покоя ![]() для системы
для системы ![]() возможно,
причём точка покоя
возможно,
причём точка покоя ![]() неустойчива.
неустойчива.
Эти теоремы не охватывают все возможные случаи. Так, они не работают, если у матрицы A все собственные значения с неположительной вещественной частью и есть собственное значение с нулевой вещественной частью. Такой случай называется критическим. В критическом случае исследование на устойчивость по первому приближению невозможно.
На
неустойчивость либо неустойчивость точки покоя ![]() оказывают
влияние только знаки вещественных частей собственных значений матрицы A, но
не модули этих собственных значений. Отсюда следует, что для исследования на
устойчивость достаточно установить знаки вещественных частей собственных
значений, не решая векового уравнения. Для этого можно воспользоваться
существующими критериями, например, критерием Гурвица.
оказывают
влияние только знаки вещественных частей собственных значений матрицы A, но
не модули этих собственных значений. Отсюда следует, что для исследования на
устойчивость достаточно установить знаки вещественных частей собственных
значений, не решая векового уравнения. Для этого можно воспользоваться
существующими критериями, например, критерием Гурвица.
§5.4 Прямой (второй) метод Ляпунова
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.