Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 27

Составим характеристическую систему для этого уравнения: 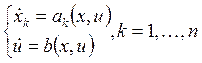. Пусть  – функционально независимые первые интегралы этой системы. Тогда  – общее решение уравнения.

Пусть  – решение уравнения 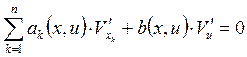 и пусть уравнение  определяет некоторую функцию  в  (пространстве x), причём . Тогда  – решение первого уравнения.

Приведённая теорема устанавливает связь между решениями уравнени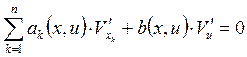й  и . Решения первого уравнения могут использоваться для неявного задания решений уравнения второго уравнения. Если  – решение первого уравнения, то конечное уравнение  определяет решение второго уравнения. Множество решений первого уравнения представляется функцией , следовательно, множество решений второго уравнения можно описать решениями уравнения , где F – произвольная функция. Следует иметь в виду, что функция F должна обеспечить возможность разрешения такого уравнения (см. теорему о неявной функции). На даже в этом случае мы не можем утверждать, что таким образом описываются все решения уравнения . Это уравнение может иметь т.н. специальные решения, не допускающие такого представления.

Характеристическая система, записанная для вспомогательного ура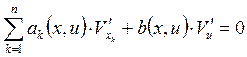внения  называется характеристической системой исходного уравнения. Через каждую точку в области проходит единственная характеристика уравнения . В отличие от предыдущего параграфа, характеристики здесь являются линиями в пространстве переменных . Можно показать, что если через какую-либо точку интегральной поверхности проходит характеристика, то вся эта характеристика лежит на интегральной поверхности. Интегральная поверхность как бы «соткана» из характеристик.

§6.4. Решение задачи Коши для квазилинейных уравнений

Рассмотрим уравнение 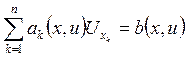, предполагая, что  и  определены в области , непрерывны и непрерывно дифференцируемы в D и  в D. Можно осуществить выбор решения этого уравнения, подчинив его каким-либо дополнительным условиям. В простейшем случае такими условиями могут быть условия Коши. Рассмотрим постановку задачи Коши. Пусть в пространстве x задана гиперповерхность S:  и пусть в точке этой гиперповерхности определена функция . Дополним уравнение условием: . Имеем задачу Коши. Решить её значит найти решение уравнения 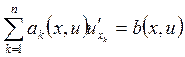, которое в точке гиперповерхности S совпадает с заданной функцией . Нас интересует интегральная поверхность этого уравнения, содержащая гиперповерхность S относительно функции .

Заметим, что в общем случае задача Коши может оказаться разрешимой однозначно, разрешимой, но не однозначно, или неразрешимой. Всё зависит от выбора гиперповерхности S и начальной функции . Следует иметь в виду, что при сколь угодно гладкой функции  решение может и не существовать.

Простейшим методом решения задачи Коши является использование общего решения уравнения с последующим удовлетворением начальных условий (если его удаётся построить).

Дополнение: решение уравнений с помощью рядов.

Рассмотрим уравнение  в окрестности точки .

Пусть коэффициенты  и  аналитичны в окрестности точки , причём . Тогда решения уравнения  аналитичны в окрестности точки  и могут быть построены в виде ряда .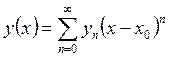

Аналитичность означает сходимость ряда Тейлора в окрестности точки . Для нахождения коэффициентов разложения решения этого уравнения степенной ряд формально подставляется в уравнение и собираются коэффициенты при одинаковых степенях. Получается некоторое рекуррентное соотношение, из которого можно найти коэффициенты.

Пусть коэффициенты уравнения  аналитичны в окрестности точки , причём , где  имеет в точке  нуль порядка  (если ),  имеет в точке  нуль порядка  (если ). Тогда это уравнение имеет по крайней мере одно решение, представляемое обобщённым степенным рядом 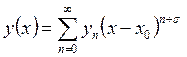, где s – любая постоянная.

Рассмотрим для примера уравнение Бесселя n-го порядка: . Здесь . Можно искать решение в виде обобщённого ряда 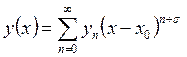, следовательно, решения такого вида существуют при 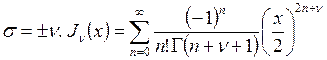 – функция Бесселя n-го порядка. Аналогично 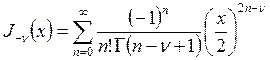. При дробных n функции  и  линейно независимы, следовательно, они образуют ФСР: . При целых , следовательно, они линейно зависимы.

В качестве второго линейного независимого решения выбираем функцию Неймана . Определим её при дробных 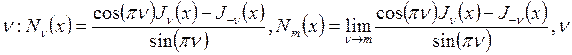 – дробное. Функции  и  линейно независимы при , как целых, так и дробных, следовательно, они образуют ФСР и общее решение: .