Можно
предложить ещё один способ решения систем уравнений с постоянными
коэффициентами. Он позволяет решать и неоднородные системы ![]() : делаем замену
: делаем замену ![]() , где C – невырожденная
постоянная матрица.
, где C – невырожденная
постоянная матрица. ![]() . Выбираем C таким, что
. Выбираем C таким, что ![]() – наиболее простая матрица, например,
диагональная.
– наиболее простая матрица, например,
диагональная.
Решения неоднородных линейных систем. Метод вариации постоянных. Матрица Коши.
Рассмотрим неоднородную систему ![]() .
.
Пусть ![]() – фундаментальные системы решений,
соответствующие системе
– фундаментальные системы решений,
соответствующие системе ![]() – частное решение
системы
– частное решение
системы ![]() . Тогда
. Тогда ![]() –
общие решения системы
–
общие решения системы ![]() , где
, где ![]() – произвольное
постоянные.
– произвольное
постоянные.
Общее
решение неоднородной системы ![]() представляется суммой
частного решения и общего решения соответствующей неоднородной системы.
представляется суммой
частного решения и общего решения соответствующей неоднородной системы.
Решить неоднородную систему ![]() можно, если подобрать какое-либо частное
решение этой системы и решить соответствующую однородную систему. Если частное
решение подобрать не удаётся, можно воспользоваться методом вариации
произвольных постоянных.
можно, если подобрать какое-либо частное
решение этой системы и решить соответствующую однородную систему. Если частное
решение подобрать не удаётся, можно воспользоваться методом вариации
произвольных постоянных.
Пусть уже построена ФСР
соответствующей однородной системы. Тогда её общее решение имеет вид ![]() . Полагая
. Полагая ![]() ,
будем искать решения системы в виде
,
будем искать решения системы в виде ![]() :
: ![]() , т.к.
, т.к. ![]() .
Введём матрицу
.
Введём матрицу ![]() составив её из всех столбцов
составив её из всех столбцов ![]() . Тогда уравнение запишется в виде
. Тогда уравнение запишется в виде 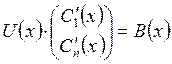 . Заметим, что
. Заметим, что ![]() при
при ![]() , следовательно,
, следовательно, 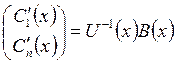 .
Интегрируя, получаем:
.
Интегрируя, получаем: 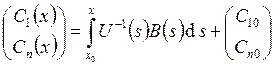 , где
, где ![]() . Заметим, что формула
. Заметим, что формула ![]()
![]() приводится к виду
приводится к виду 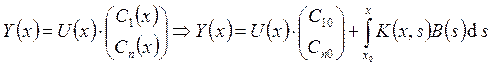 , где
, где ![]() –
матрица Коши. Здесь
–
матрица Коши. Здесь 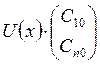 – общее решение соответствующей
однородной системы, а
– общее решение соответствующей
однородной системы, а 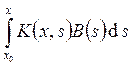 – частное решение
неоднородной системы.
– частное решение
неоднородной системы.
![]() . При фиксированном s матрицу
Коши можно понимать как матричное решение уравнения
. При фиксированном s матрицу
Коши можно понимать как матричное решение уравнения ![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию ![]() .
.
Глава 5. Устойчивость решений дифференциальных уравнений
§5.1 Понятие устойчивости по Ляпунову. Асимптотическая устойчивость. Точки покоя.
Рассмотрим систему
дифференциальных уравнений ![]() порядка
порядка ![]() . Предполагается, что
. Предполагается, что ![]() определена при
определена при ![]() и
и ![]() и что выполнены условия теоремы
существования и единственности решения. Будем полагать, что система
и что выполнены условия теоремы
существования и единственности решения. Будем полагать, что система ![]() имеет решение
имеет решение ![]() определённое
при
определённое
при ![]() .
.
Решение
![]() называется устойчивым (по Ляпунову), если
для
называется устойчивым (по Ляпунову), если
для ![]() при
при ![]() для
любого решения
для
любого решения ![]() , в начальный момент
, в начальный момент ![]() удовлетворяющего условию
удовлетворяющего условию ![]() .
.
Решение
![]() называется притягивающим при
называется притягивающим при ![]() , если
, если ![]() для
любого решения
для
любого решения ![]() .
.
Решение
![]() называется асимптотически устойчивым, если
оно устойчиво и является притягивающим.
называется асимптотически устойчивым, если
оно устойчиво и является притягивающим.
Решение
![]() , которое не является устойчивым, будем
называть неустойчивыми.
, которое не является устойчивым, будем
называть неустойчивыми.
Обычно исследование на
устойчивость произвольного решения ![]() сводят к исследованию
на устойчивость тривиального решения. В противном случае можно сделать замену
сводят к исследованию
на устойчивость тривиального решения. В противном случае можно сделать замену ![]() в уравнении
в уравнении ![]() .
Решению
.
Решению ![]() соответствует
соответствует ![]()
![]() . Т.к.
. Т.к. ![]() , то
, то ![]() , где
, где ![]()
![]() . Заметим, что
. Заметим, что ![]() .
.
Исследуем
на устойчивость ![]() в фазовом пространстве системы
в фазовом пространстве системы ![]() . Всякому постоянному решению отвечает
точка. Такие точки мы будем называть точками покоя системы
. Всякому постоянному решению отвечает
точка. Такие точки мы будем называть точками покоя системы ![]() .
.
Все предыдущие определения легко
переносятся в фазовые пространства. В этом случае можно говорить об устойчивых
точках покоя, асимптотически устойчивых точках покоя, неустойчивых точках покоя.
Если надо исследовать при ![]() , то можно сделать
замену
, то можно сделать
замену ![]() .
.
§5.2 Простейшие типы точек покоя на плоскости
Будем рассматривать систему 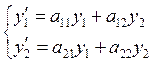 в векторной форме:
в векторной форме: 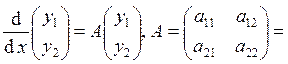
![]() . Точки покоя этой системы можно найти,
решая систему
. Точки покоя этой системы можно найти,
решая систему 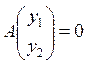 . Если
. Если ![]() ,
то эта система имеет единственное решение
,
то эта система имеет единственное решение ![]() , иначе
система имеет бесконечное множество решений. Ограничимся случаем
, иначе
система имеет бесконечное множество решений. Ограничимся случаем ![]() .
.
1.  Пусть
Пусть ![]() и
и ![]() –
собственные числа,
–
собственные числа, ![]() и
и ![]() –
соответствующие им собственные векторы. Общее решение системы представляется в
виде
–
соответствующие им собственные векторы. Общее решение системы представляется в
виде 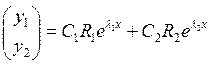 .
.
а)
![]() точка
покоя
точка
покоя ![]() асимптотически устойчива. Называется
устойчивым узлом.
асимптотически устойчива. Называется
устойчивым узлом.
б)
![]() .
Фазовый портрет подобен предыдущему, но направление движения противоположно.
Точка покоя
.
Фазовый портрет подобен предыдущему, но направление движения противоположно.
Точка покоя ![]() неустойчива
и называется неустойчивым узлом.
неустойчива
и называется неустойчивым узлом.
в)

![]() (второй
рисунок). Точка покоя
(второй
рисунок). Точка покоя ![]() является неустойчивой и
называется седлом.
является неустойчивой и
называется седлом.
2. Пусть A имеет комплексные собственные числа: ![]() ,
, ![]() и
и ![]() – соответствующие им собственные векторы.
Тогда общее решение будет записываться в виде:
– соответствующие им собственные векторы.
Тогда общее решение будет записываться в виде: 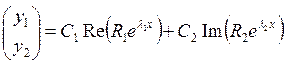 .
Удобнее записать его несколько иначе:
.
Удобнее записать его несколько иначе: 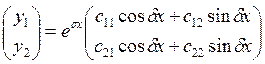 (здесь
(здесь
![]() – линейная комбинация
– линейная комбинация ![]() и
и ![]() ).
).
a)
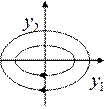
![]() Точка покоя
Точка покоя ![]() устойчива. Асимптотической устойчивости
нет. Точка покоя называется центром.
устойчива. Асимптотической устойчивости
нет. Точка покоя называется центром.
б) ![]() В первом
случае
В первом
случае ![]() точка покоя
точка покоя ![]() называется
устойчивым фокусом. Она асимптотически устойчива. Во втором случае
называется
устойчивым фокусом. Она асимптотически устойчива. Во втором случае ![]() точка покоя
точка покоя ![]() называется неустойчивым
фокусом.
называется неустойчивым
фокусом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.