4. Пусть
уравнение ![]() имеет простые вещественные корни
имеет простые вещественные корни ![]() . Тогда матрица A
имеет простые собственные значения
. Тогда матрица A
имеет простые собственные значения ![]() . Каждому
. Каждому ![]() сопоставляем собственный вектор
сопоставляем собственный вектор ![]() . Имеем собственные векторы
. Имеем собственные векторы ![]() . Они линейно независимы. По формуле
. Они линейно независимы. По формуле ![]() получаем решение системы
получаем решение системы ![]() . Эти решения линейно независимы (т.к.
определитель Вронского отличен от 0), их n,
следовательно, они образуют ФСР. Общее решение системы
. Эти решения линейно независимы (т.к.
определитель Вронского отличен от 0), их n,
следовательно, они образуют ФСР. Общее решение системы 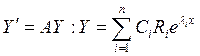 .
.
5. Корни
характеристического уравнения ![]() простые, но среди них
есть комплексные. Пусть
простые, но среди них
есть комплексные. Пусть ![]() – корни уравнения
– корни уравнения ![]() . Они являются собственными значениями
матрицы A. Пусть
. Они являются собственными значениями
матрицы A. Пусть ![]() –
какой-либо корень. Если он вещественный, то по формуле
–
какой-либо корень. Если он вещественный, то по формуле ![]() получаем
решение:
получаем
решение: ![]() . Пусть теперь
. Пусть теперь ![]() –
комплексный корень,
–
комплексный корень, ![]() . Тогда в силу вещественности
матрицы A существует ещё один корень
. Тогда в силу вещественности
матрицы A существует ещё один корень ![]() . Этим комплексным значениям соответствуют
комплексные собственные векторы
. Этим комплексным значениям соответствуют
комплексные собственные векторы ![]() и
и ![]() , причём
, причём ![]() ,
следовательно, корням
,
следовательно, корням ![]() и
и ![]() сопоставляется
комплексные решения
сопоставляется
комплексные решения ![]() и
и ![]() . При
этом
. При
этом ![]() ,
, ![]() .
Выбираем
.
Выбираем ![]() . В итоге двум комплексным корням
поставлены в соответствие два вещественных решения. Разбираясь таким образом с
каждым корнем уравнения
. В итоге двум комплексным корням
поставлены в соответствие два вещественных решения. Разбираясь таким образом с
каждым корнем уравнения ![]() , получаем n решений. Эти решения линейно независимы, следовательно,
они образуют ФСР, следовательно, можно записать общее решение системы
, получаем n решений. Эти решения линейно независимы, следовательно,
они образуют ФСР, следовательно, можно записать общее решение системы ![]() .
.
6. Пусть
уравнение ![]() имеет корни
имеет корни ![]() ,
соответственно, кратности
,
соответственно, кратности ![]() . Имеем
. Имеем ![]() . Если
. Если ![]() , то все корни простые. Этот случай
уже рассмотрен. Пусть
, то все корни простые. Этот случай
уже рассмотрен. Пусть![]() , тогда существует хотя бы один
корень
, тогда существует хотя бы один
корень ![]() кратности
кратности ![]() .
По-прежнему сопоставляем каждому корню решения системы
.
По-прежнему сопоставляем каждому корню решения системы ![]() ,
число которых равно кратности корня. Поскольку
,
число которых равно кратности корня. Поскольку ![]() –
кратный корень, ему можно сопоставить по формуле
–
кратный корень, ему можно сопоставить по формуле ![]() в общем
случае несколько решений
в общем
случае несколько решений ![]() , где
, где ![]() – линейно независимые собственные векторы,
соответствующие собственному значению
– линейно независимые собственные векторы,
соответствующие собственному значению ![]() . Если
. Если ![]() , недостающие решения можно искать в виде
, недостающие решения можно искать в виде ![]() , где
, где ![]() –
неопределённые постоянные векторные коэффициенты (удобнее взять
–
неопределённые постоянные векторные коэффициенты (удобнее взять 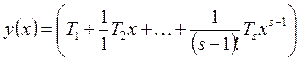 ). Выбирая
). Выбирая ![]() , достраиваем
недостающие решения до
, достраиваем
недостающие решения до ![]() . Поступая таким образом с каждым
кратным корнем, получаем n решений системы
. Поступая таким образом с каждым
кратным корнем, получаем n решений системы ![]() . В общем случае эти решения комплексные.
Выделяя вещественные и мнимые части у построенных решений (как в пункте 2),
получаем n вещественных решений системы
. В общем случае эти решения комплексные.
Выделяя вещественные и мнимые части у построенных решений (как в пункте 2),
получаем n вещественных решений системы ![]() . Они линейно независимы, следовательно,
они образуют ФСР. Получаем общее решение системы
. Они линейно независимы, следовательно,
они образуют ФСР. Получаем общее решение системы ![]() .
Отметим, что можно ограничиться и выбором комплексной ФСР. В этом случае при
записи общего решения системы произвольные постоянные также должны быть
комплексными.
.
Отметим, что можно ограничиться и выбором комплексной ФСР. В этом случае при
записи общего решения системы произвольные постоянные также должны быть
комплексными.
Можно
предложить ещё один способ решения систем уравнений с постоянными
коэффициентами. Он позволяет решать и неоднородные системы ![]() : делаем замену
: делаем замену ![]() , где C – невырожденная
постоянная матрица.
, где C – невырожденная
постоянная матрица. ![]() . Выбираем C таким, что
. Выбираем C таким, что ![]() – наиболее простая матрица, например,
диагональная.
– наиболее простая матрица, например,
диагональная.
Решения неоднородных линейных систем. Метод вариации постоянных. Матрица Коши.
Рассмотрим неоднородную систему ![]() .
.
Пусть ![]() – фундаментальные системы решений,
соответствующие системе
– фундаментальные системы решений,
соответствующие системе ![]() – частное решение
системы
– частное решение
системы ![]() . Тогда
. Тогда ![]() –
общие решения системы
–
общие решения системы ![]() , где
, где ![]() –
произвольное постоянные.
–
произвольное постоянные.
Общее
решение неоднородной системы ![]() представляется суммой
частного решения и общего решения соответствующей неоднородной системы.
представляется суммой
частного решения и общего решения соответствующей неоднородной системы.
Решить неоднородную систему ![]() можно, если подобрать какое-либо частное
решение этой системы и решить соответствующую однородную систему. Если частное
решение подобрать не удаётся, можно воспользоваться методом вариации произвольных
постоянных.
можно, если подобрать какое-либо частное
решение этой системы и решить соответствующую однородную систему. Если частное
решение подобрать не удаётся, можно воспользоваться методом вариации произвольных
постоянных.
Пусть уже построена ФСР
соответствующей однородной системы. Тогда её общее решение имеет вид ![]() . Полагая
. Полагая ![]() ,
будем искать решения системы в виде
,
будем искать решения системы в виде ![]() :
: ![]() , т.к.
, т.к. ![]() .
Введём матрицу
.
Введём матрицу ![]() составив её из всех столбцов
составив её из всех столбцов ![]() . Тогда уравнение запишется в виде
. Тогда уравнение запишется в виде 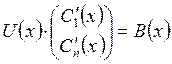 . Заметим, что
. Заметим, что ![]() при
при ![]() , следовательно,
, следовательно, 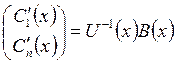 .
Интегрируя, получаем:
.
Интегрируя, получаем: 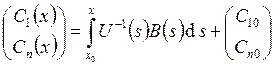 , где
, где ![]() . Заметим, что формула
. Заметим, что формула ![]()
![]() приводится к виду
приводится к виду 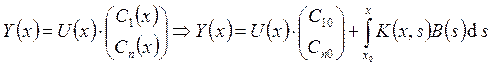 , где
, где ![]() –
матрица Коши. Здесь
–
матрица Коши. Здесь 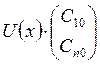 – общее решение соответствующей
однородной системы, а
– общее решение соответствующей
однородной системы, а 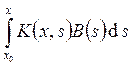 – частное решение
неоднородной системы.
– частное решение
неоднородной системы.
![]() . При фиксированном s матрицу
Коши можно понимать как матричное решение уравнения
. При фиксированном s матрицу
Коши можно понимать как матричное решение уравнения ![]() ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию ![]() .
.
Глава 5. Устойчивость решений дифференциальных уравнений
§5.1 Понятие устойчивости по Ляпунову. Асимптотическая устойчивость. Точки покоя.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.