Заметим, что в общем случае
задача Коши может оказаться разрешимой однозначно, разрешимой, но не
однозначно, или неразрешимой. Всё зависит от выбора гиперповерхности S и начальной функции ![]() .
Следует иметь в виду, что при сколь угодно гладкой функции
.
Следует иметь в виду, что при сколь угодно гладкой функции ![]() решение может и не существовать.
решение может и не существовать.
Простейшим методом решения задачи Коши является использование общего решения уравнения с последующим удовлетворением начальных условий (если его удаётся построить).
Дополнение: решение уравнений с помощью рядов.
Рассмотрим уравнение ![]() в окрестности точки
в окрестности точки ![]() .
.
Пусть
коэффициенты ![]() и
и ![]() аналитичны
в окрестности точки
аналитичны
в окрестности точки ![]() , причём
, причём ![]() .
Тогда решения уравнения
.
Тогда решения уравнения 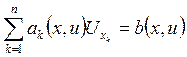 аналитичны в
окрестности точки
аналитичны в
окрестности точки ![]() и могут быть построены в виде
ряда
и могут быть построены в виде
ряда 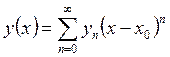 .
.
Аналитичность означает сходимость
ряда Тейлора в окрестности точки ![]() . Для нахождения
коэффициентов разложения решения этого уравнения степенной ряд формально
подставляется в уравнение и собираются коэффициенты при одинаковых степенях.
Получается некоторое рекуррентное соотношение, из которого можно найти
коэффициенты.
. Для нахождения
коэффициентов разложения решения этого уравнения степенной ряд формально
подставляется в уравнение и собираются коэффициенты при одинаковых степенях.
Получается некоторое рекуррентное соотношение, из которого можно найти
коэффициенты.
Пусть
коэффициенты уравнения 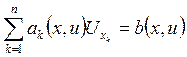 аналитичны в
окрестности точки
аналитичны в
окрестности точки ![]() , причём
, причём ![]() ,
где
,
где ![]() имеет в точке
имеет в точке ![]() нуль
порядка
нуль
порядка ![]() (если
(если ![]() ),
), ![]() имеет в точке
имеет в точке ![]() нуль
порядка
нуль
порядка ![]() (если
(если ![]() ). Тогда
это уравнение имеет по крайней мере одно решение, представляемое обобщённым
степенным рядом
). Тогда
это уравнение имеет по крайней мере одно решение, представляемое обобщённым
степенным рядом 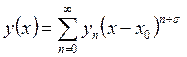 , где s
– любая постоянная.
, где s
– любая постоянная.
Рассмотрим для примера уравнение
Бесселя n-го порядка: ![]() . Здесь
. Здесь ![]() . Можно
искать решение в виде обобщённого ряда
. Можно
искать решение в виде обобщённого ряда 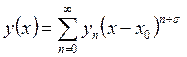 ,
следовательно, решения такого вида существуют при
,
следовательно, решения такого вида существуют при 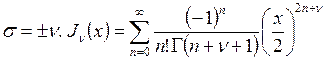 –
функция Бесселя n-го порядка.
Аналогично
–
функция Бесселя n-го порядка.
Аналогично 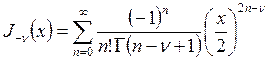 . При дробных n функции
. При дробных n функции ![]() и
и ![]() линейно независимы, следовательно, они
образуют ФСР:
линейно независимы, следовательно, они
образуют ФСР: ![]() . При целых
. При целых ![]() , следовательно, они линейно зависимы.
, следовательно, они линейно зависимы.
В качестве второго линейного
независимого решения выбираем функцию Неймана ![]() .
Определим её при дробных
.
Определим её при дробных 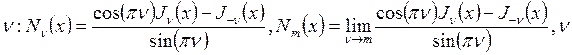 – дробное. Функции
– дробное. Функции ![]() и
и ![]() линейно
независимы при
линейно
независимы при ![]() , как целых, так и дробных,
следовательно, они образуют ФСР и общее решение:
, как целых, так и дробных,
следовательно, они образуют ФСР и общее решение: ![]() .
.
ча имеет нетривиальное решение называется собственным значением этой краевой задачи, а нетривиальные решения, соответствующие собственным значениям, называются собственными функциями этой краевой задачи.
Таким образом, задача переходит в задачу на собственные значения, или задачу Штурма-Лиувилля. Решить задачу на собственные значения значит найти все собственные значения и собственные функции этой задачи.
Свойства собственных значений и собственных функций:
6. Собственные значения существуют и их счётное множество.
7. Собственные значения вещественны.
8.
В случае ![]() и
и ![]() все собственные значения положительны.
все собственные значения положительны.
9. Ранг каждого собственного значения равен 1, т.е. любому собственному значению соответствует только одна линейно независимая собственная функция.
10. Собственные функции, соответствующие различным собственным
числам ортогональны с весом ![]() , т.е.
, т.е. 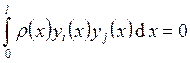 , где
, где ![]() и
и ![]() – собственные функции, соответствующие
собственным значениям
– собственные функции, соответствующие
собственным значениям ![]() (т.е.
(т.е. 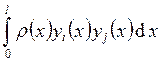 –
скалярное произведение
–
скалярное произведение ![]() ).
).
Теорема Стеклова: Любую непрерывную дважды дифференцируемую на ![]() функцию
функцию ![]() ,
удовлетворяющую условиям
,
удовлетворяющую условиям 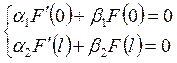 можно разложить в
абсолютно и равномерно сходящийся ряд по собственным функциям краевой задачи:
можно разложить в
абсолютно и равномерно сходящийся ряд по собственным функциям краевой задачи: ![]() (обобщённый ряд Фурье), где
(обобщённый ряд Фурье), где 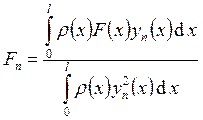 (коэффициенты Фурье).
(коэффициенты Фурье).
Доказательство 4-го свойства:
Предположим, что собственному значению ![]() соответствуют
линейно независимые
соответствуют
линейно независимые ![]() и
и ![]() . Тогда
. Тогда ![]() и
и ![]() –
решение уравнения при
–
решение уравнения при ![]() и, т.к. они линейно независимы,
то они образуют ФСР, следовательно,
и, т.к. они линейно независимы,
то они образуют ФСР, следовательно, ![]() на
на ![]() . С другой стороны,
. С другой стороны, ![]() и
и
![]() удовлетворяют краевым условиям. Рассмотрим
условия при
удовлетворяют краевым условиям. Рассмотрим
условия при ![]() ,
, ![]() . Имеем
систему уравнений относительно
. Имеем
систему уравнений относительно ![]() , которая имеет
нетривиальное решение
, которая имеет
нетривиальное решение ![]() , следовательно, матрица этой
системы вырожденная:
, следовательно, матрица этой
системы вырожденная: 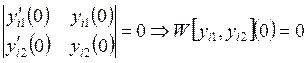 , следовательно, двух линейно
независимых функций быть не может.
, следовательно, двух линейно
независимых функций быть не может.
Глава 4. Системы дифференциальных уравнений.
§4.1 Нормальные системы.
В общем случае систему
дифференциальных уравнений можно представить в виде ![]() . Имеем
систему k уравнений относительно m неизвестных.
. Имеем
систему k уравнений относительно m неизвестных.
Введём:
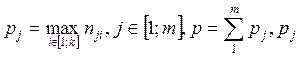 – порядок системы относительно неизвестной
– порядок системы относительно неизвестной
![]() , а p общий порядок
системы.
, а p общий порядок
системы.
Пусть
система приводится к виду 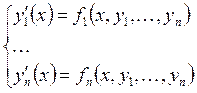 . Эта система называется
нормальной системой, порядок её равен n.
. Эта система называется
нормальной системой, порядок её равен n.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.