Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 26

Вторая теорема допускает прямое обращение: если второе условие заменить противоположным: , то получится теорема Ляпунова о неустойчивости точки покоя . Однако теорема Ляпунова о неустойчивости получается при слишком жёстких условиях. Так, сколь угодно малую окрестность точки покоя  должна покидать любая траектория системы, в то время как для доказательства неустойчивости достаточно показать, что хотя бы одна траектория покидает такую окрестность. Такое более тонкое исследование можно провести с помощью теорем типа теоремы Четаева.

Глава 6. Уравнения с частными производными первого порядка.

§6.1. Основные определения.

В общем случае уравнение с частными производными первого порядка имеет вид: . Здесь 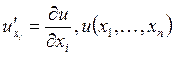 – неизвестная функция. Далее будем обозначать: . Тогда .

Если уравнение представляется в виде: 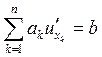, где  и , то уравнение называется квазилинейным.

Если , а , то уравнение называется линейным. При этом линейное уравнение называется однородным, если , иначе – неоднородным. Соответственно,  – неоднородность линейного уравнения.

Гиперповерхность – это поверхность, размерность которой на единицу меньше, чем размерность рассматриваемого пространства.

Геометрически неизвестной функции  в пространстве переменных  соответствует некоторая гиперповерхность. Если  – решение дифференциального уравнения, то такая гиперповерхность называется интегральной поверхностью уравнения.

Под решением уравнения с частными производными будем понимать непрерывную и непрерывно дифференцируемую функцию, которая при подстановке её в уравнение превращает его в верное тождество.

§6.2. Решение однородных линейных уравнений

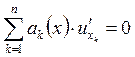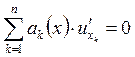Рассмотрим уравнение  в предположении, что все коэффициенты  определены в некоторой области D пространства , непрерывны и непрерывно дифференцируемы в D, причём  в D. Введём вектор . Составим вектор  и тогда уравнение  примет вид:  если  – решение уравнения 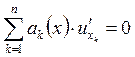, то производная этого решения по направлению  в каждой точке равна 0.

 задаёт векторное поле в области D. Векторные линии этого векторного поля являются фазовыми траекториями системы уравнений 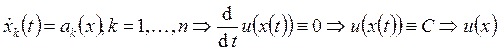 – первый интеграл системы . Мы установили: всякое решение уравнения 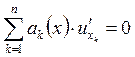 является первым интегралом системы . Верно и обратное: всякий первый интеграл системы  является решением уравнения 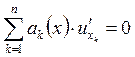, следовательно, чтобы описать всё множество решений этого уравнения достаточно описать множество первых интегралов системы .

Система  называется характеристической системой уравнения .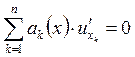

Фазовые траектории этой системы называется характеристиками этого уравнения.

Через любую точку области D проходит единственная характеристика (система автономна). Точек покоя эта система не имеет. В этом случае всякая точка области D является регулярной.

Для того, чтобы описать все первые интегралы системы , необходимо получить полный набор функционально независимых первых интегралов . Отметим, что  функционально независимы, если ранг матрицы . Для системы , состоящей из n уравнений, полный набор состоит из n функционалов вида . Если рассматриваются первые интегралы вида , то полный набор состоит из  первого интеграла. В общем случае для наперёд заданной области D полный набор первых интегралов может и не существовать. Однако справедливо следующее утверждение: для любой нерегулярной точки найдется окрестность, в которой существует полный набор функционально независимых первых интегралов. Пусть D – такая окрестность, в котором существует полный набор первых интегралов. Следовательно, имеем первые интегралы , следовательно, для любого первого интеграла  справедливо представление: , где F – некоторая функции, следовательно, любое решение уравнения 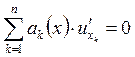 представляется в виде . Эта формула задаёт общее решение уравнения при произвольной дифференцируемой функции F.

Характеристическую систему  удобно представлять в форме: .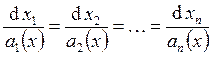

§6.3. Решение квазилинейных уравнений

Рассмотрим уравнение  в предположении, что  и  определены в области , непрерывны и непрерывно дифференцируемы в D, причём 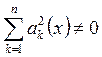 в D. Сопоставим этому уравнению вспомогательное линейное уравнение 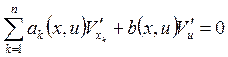. Здесь . Это уравнение уже рассмотрено в предыдущем параграфе, следовательно, можно написать его общее решение. Оно получается в неявном виде: .