Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 3

Следовательно, решение задачи Коши легко получить соответствующим . Общее решение неоднородного линейного уравнения, представляющееся суммой общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного линейного уравнения, можно получить, решив соответствующее однородное уравнение и подобрав каким-либо образом частное решение неоднородного уравнения.

Общие свойства линейных уравнений:

1.  Пусть  – решение уравнения . Тогда  – тоже решение этого же уравнения.

2.  Пусть  и  – решения уравнения . Тогда  – тоже решения этого же уравнения.

3.  Принцип суперпозиции: пусть в неоднородном уравнении  и  – решение уравнения . Тогда  – решение уравнения .

§ 1.5 Теорема о существовании и единственности решения задачи Коши для уравнения, разрешённого относительно производной

Рассмотрим уравнение , предполагая, что  определена в области D. Зафиксируем точку  и дополним уравнение начальным условием . В результате получим задачу Коши.

Пусть функция  непрерывна в D, причём в любой ограниченной замкнутой подобласти  удовлетворяет условию Липшица: , где L – постоянная Липшица, . Тогда найдётся отрезок  и , на котором наша задача Коши имеет единственное решение.

Эта теорема часто называется теоремой Пикара. В ней непрерывность функции  обеспечивает существование решения, а условие Липшица отвечает за его единственность.

При условиях теоремы уравнение  имеет единственное решение вида , где C – произвольная постоянная.

Приведённая теорема позволяет выделять множество так называемых обыкновенных точек:

Точка  называется обыкновенной (регулярной) точкой уравнения , если найдётся окрестность этой точки, через каждую точку которой проходит единственная интегральная линия уравнения.

Точка , не являющаяся обыкновенной, называется особой точкой уравнения.

Особые точки:

1.  Граничные точки.

2.  Точки неединственности.

3.  Предельные точки для множества особых.

Особая точка  называется изолированной, если найдётся окрестность этой точки, в которой нет других особых точек. В противном случае она называется неизолированной.

Если из особых точек составлена линия, то такая линия называется особой линией. Если особая линия является интегральной линией, то она называется особой интегральной линией.

Решение уравнения, соответствующее особой интегральной линии – особое решение.

Классическим примером особой интегральной линии является огибающая семейства интегральных линий (например,  в уравнении ).

§ 1.6 Уравнения, не разрешённые относительно производных.

В общем случае уравнения первого порядка представляются в виде .

Уравнением, не разрешённым относительно производной, называют уравнение вида , которое не удаётся свести к виду .

Рассмотрим уравнение вида , предполагая, что  определена в некоторой области . Пусть точка : найдётся такое p, что . Дополнив уравнение начальным условием , получим задачу Коши.

Задача Коши называется корректно поставленной, если через точку  проходит конечное число интегральных линий уравнения , имеющих различные угловые коэффициенты.

В случае, когда задача Коши поставлена корректно, решение этой задачи можно выделить однозначно, дополнительно указав угловой коэффициент. Выбор углового коэффициента можно произвести, решая конечное уравнение  относительно p. Тогда p и есть угловой коэффициент.

Пусть  непрерывна в D и имеет непрерывные производные  и . Пусть также в точке . Тогда задача Коши имеет единственное решение на некотором , удовлетворяющее условию .

Методы решения:

1.  Прямое разрешение уравнения . Результат – система уравнений 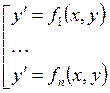. Решая эту систему, находим решение исходного уравнения.

2.  Параметризация. Интегральные линия уравнения описываются в параметрическом виде. В простейших случаях можно обойтись одним параметром: . Так решаются, например, уравнение Клеро  и уравнение Лагранжа .

Для уравнений, неразрешённых относительно производной также можно ввести понятие особой точки, особого решения.

Глава 2. Уравнения порядка выше первого.