Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 6

Таким образом, существует взаимно однозначное соответствие между уравнениями и пространствами решений. Предположим теперь, что исходное уравнение известно: 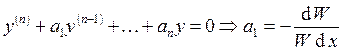. Интегрируя, получаем: 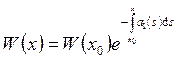 – формула Остроградского-Лиувилля. Её можно использовать для понижения порядка уравнения, если известно хотя бы одно нетривиальное решение этого уравнения. Тем самым иногда удаётся решить уравнение с переменными коэффициентами.

§2.6 Решения неоднородных линейных уравнений. Метод вариации произвольных переменных. Функция Коши.

Рассмотрим неоднородное уравнение .

Пусть  – ФСР уравнения  – любое частное решение неоднородного уравнения . Тогда общее решение уравнения  представляется в виде .

Пусть  – произвольное решение уравнения . Имеем два решения:  и , следовательно,  – решение соответствующего однородного уравнения  существуют постоянные , при которых , т.е. . Т.к.  – произвольно, то все решения можно представить так: .

1.  Общее решение неоднородного линейного уравнения представляется суммой частного решения этого уравнения и общего решения соответствующего однородного уравнения.

2.  Общее решение неоднородного линейного уравнения можно получить, решив соответствующее однородное уравнение и подобрав каким-либо образом частное решение неоднородного уравнения.

Если частное решение подобрать не удаётся, это уравнение можно решить методом вариации произвольных постоянных:

Положим, что ФСР соответствующего однородного уравнения  построена. Общее решение соответствующего однородного уравнения имеет вид: . Варьируем произвольные постоянные: . Будем искать решение уравнения  в виде : вычисляем производную , и требуем, чтобы . Вычисляем вторую производную: , и требуем, чтобы . …. Вычисляем -ю производную: , и требуем, чтобы . Вычисляем n-ю производную:  . Подставим теперь вычисленные производные в уравнение: 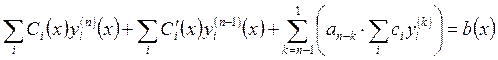. Т.к. 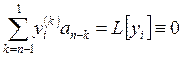, то . Соберём все полученные соотношения в систему: 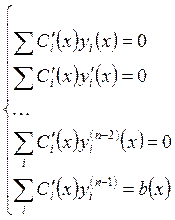. В результате мы имеем систему алгебраических линейных уравнений относительно . Это неоднородная система с невырожденной матрицей, т.к. её определитель совпадает с  (т.к.  – ФСР), следовательно, система имеет единственное решение при любой функции . Пусть это решение представляется в виде . Тогда 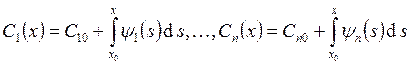. Подставляя эти функции в формулу , получим: 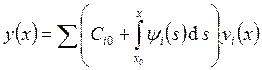. Уточним вид функции . Решая систему по правилу Крамера, замечаем, что 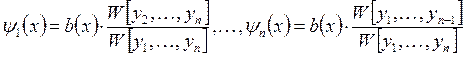, т.е. определяется только . В результате имеем: 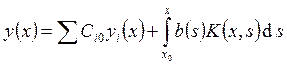, где 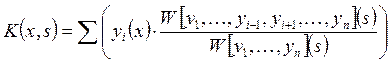. Функция  называется функцией Коши. 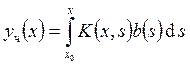 – частное решение неоднородного уравнения, но в то же время  – решение соответствующего однородного уравнения, если её рассматривать как функцию x при фиксированном s. При этом её можно получить, решая задачу Коши для однородного уравнения с начальными условиями при .

Если рассматривается уравнение , то в системе в последнем уравнении следует заменить  на .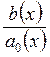

Глава 3. Краевые задачи для линейного уравнения второго порядка

Рассмотрим уравнение . Ранее такое уравнение изучалось на  в предположении непрерывности функций  и  на , строилось общее решение. Для однородного уравнения (при ) строилась ФСР. При этих условиях задача Коши для нашего уравнения с начальными условиями , где  – фиксированная точка из , а  и  – заданные числа, всегда однозначно разрешима. Всё приведённое сохраняется, если вместо  рассматривается .

В этой главе нас интересует краевые задачи для уравнения . Это значит, что дополнительные условия мы будем ставить в граничных точка промежутка. В этом случае, несмотря на то, что задача Коши для этого уравнения всегда однозначно разрешима, краевая задача может оказаться неразрешимой, разрешимой неоднозначно или однозначно разрешимой.

В дальнейшем будем рассматривать вместо этого уравнения уравнение  на . Будем полагать, что функции  определены и непрерывны на  и  на .

Приведённые условия позволяют легко перейти от первого уравнения ко второму. Действительно, 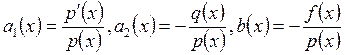. Возможен и обратный переход: домножим первое уравнение на 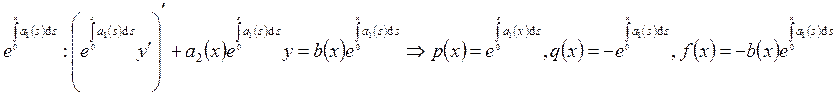. Отсюда следует, что вся предыдущая теория переносится на уравнения второго вида.