Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 22

Предположим, что функции  определены в некоторой области . Фиксируем точку  и добавляем начальные условия: .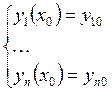

Пусть функции  непрерывны в D и непрерывно дифференцируемы по . Тогда найдётся такой отрезок  и , на котором задача Коши имеет единственное решение. Отметим, что решением системы называется совокупность функций , непрерывных и непрерывно дифференцируемых, которые, будучи подставленными в систему, превращают эту систему в систему тождеств.

При условиях теоремы общее решение системы имеет вид .

Геометрически решениям системы отвечает линия в пространстве переменных , называемая интегральной линией. Общему решению системы ставится в соответствие семейство интегральных линий. При условиях теоремы интегральные линии не пересекаются.

Пространство переменных  называется фазовым пространством системы. Проекция интегральной линии на фазовое пространство называется фазовой траекторией системы. При этом обычно указывается также и направление движения по фазовой траектории при возрастании аргумента x. В общем случае даже при условиях теоремы фазовые траектории могут пересекаться.

Система 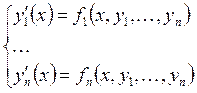 называется автономной, если в правой части  (не зависят явным образом от x).

Фазовые траектории автономной системы при условиях теоремы не пересекаются.

Совокупность фазовых траекторий системы называется фазовым портретом этой системы.

Системы уравнений вида 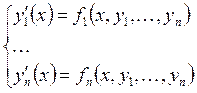 оказывается удобным записывать в векторной форме: 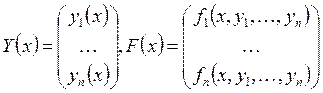. Тогда эта система приводится к виду . Здесь .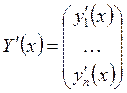

§1.2 Линейные системы. Общие свойства линейных систем.

Рассмотрим системы вида . Такие системы будем называть линейными. Здесь A – матрица системы (матрица коэффициентов системы). Если A – постоянна, то эта система называется системой с постоянными коэффициентами, иначе – системой с переменными коэффициентами. Векторная функция  – это неоднородность системы. Если , то система однородна, иначе – неоднородна.

Будем использовать обозначения: 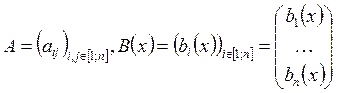. Будем полагать, что  и  определены на .

Дополним систему условием: , где  – фиксирована. Имеем задачу Коши. Пусть  и  непрерывны на . Тогда задача Коши имеет единственное решение на всём .

Общие свойства линейных систем:

6.  Если  – решение системы , то  – тоже решение этой системы при любом постоянном С.

7.  Если  и  – решения системы , то  – тоже решение этой системы.

8.  (Принцип суперпозиции) Пусть  и пусть  – решение системы . Тогда  – решение системы .

9.  Пусть  – решения системы . Тогда 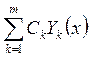 – решения этой же системы при любых постоянных .

10.  Пусть  – любое частное решение системы  – решение системы . Тогда  – решение системы .

Пусть система имеет комплексное решение . Тогда функции  и  будут вещественными решениями этой системы.

§4.3 Решение однородных линейных систем

Пусть рассматривается система векторных функций . Эта система называется линейно независимой, если  тогда и только тогда, когда , иначе система называется линейно зависимой.

3.  Если  – линейно зависимые решения системы, то определитель Вронского .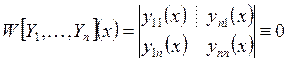

4.  Если  линейно независимые решения системы , то .

Система линейно независимых решений системы  порядка n называется фундаментальной системой решений (ФСР).

Функции ФСР получаются при решении задачи Коши.

Пусть  – ФСР системы . Тогда 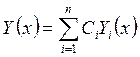 – общее решение. Здесь  – любые постоянные.

Чтобы получить общее решение системы достаточно построить ФСР этой системы. В общем случае переменных коэффициентов общего метода построения ФСР в элементарных функциях нет. В случае постоянных коэффициентов ФСР системы можно получить всегда.

§4.1. Решение однородных линейных систем с постоянными коэффициентами

Рассмотрим систему уравнений , где . Будем искать решение в виде . Подставляем ,  – собственный вектор, а l –  собственное значение матрицы A. Собственные значения – корни характеристического (векового) уравнения . Это алгебраическое уравнение относительно l степени n.