Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 25

Рассмотрим произвольную нелинейную систему . Предположим, что  определена при . Пусть для этой системы выполнены условия теоремы существования и единственности и  на . Последнее условие обеспечивает существование точки покоя . Далее будем полагать, что функция  в окрестности точки  допускает разложение , где  имеет оценку: , где M и g – положительные постоянные. Сопоставим системе линейную систему .  Эта система называется системой первого приближения, для первоначальной системы.

Система первого приближения называется стационарной, если матрица A постоянна.

Точка покоя  системы  является также точкой покоя и системы первого приближения.

Будем говорить, что система  допускает исследование точки покоя  на устойчивость по первому приближению, если эта точка является одновременно устойчивой (неустойчивой), как для системы , так и для системы .

В случае, когда система  допускает исследование на устойчивость по первому приближению, это исследование можно провести для более удобной системы .

Пусть  допускает разложение , где  имеет оценку: , где M и g – положительные постоянные. Пусть при этом система первого приближения  стационарна. Тогда

3.  (теорема об устойчивости): Если все собственные значения матрицы A имеют отрицательную вещественную часть, то исследование на устойчивость по первому приближению точки покоя  для системы  возможно, причём точка покоя  асимптотически устойчива.

4.  (теорема о неустойчивости): Если хотя бы одно собственное значение имеет положительную вещественную часть, то исследование на неустойчивость по первому приближению точки покоя  для системы  возможно, причём точка покоя  неустойчива.

Эти теоремы не охватывают все возможные случаи. Так, они не работают, если у матрицы A все собственные значения с неположительной вещественной частью и есть собственное значение с нулевой вещественной частью. Такой случай называется критическим. В критическом случае исследование на устойчивость по первому приближению невозможно.

На неустойчивость либо неустойчивость точки покоя  оказывают влияние только знаки вещественных частей собственных значений матрицы A, но не модули этих собственных значений. Отсюда следует, что для исследования на устойчивость достаточно установить знаки вещественных частей собственных значений, не решая векового уравнения. Для этого можно воспользоваться существующими критериями, например, критерием Гурвица.

§5.4 Прямой (второй) метод Ляпунова

Пусть система  определена при  и эта система имеет точку покоя . Заметим, что в этом случае . Будем говорить, что функция , определённая в D, положительно определена, если  и  при . Пример: .

Первая теорема Ляпунова: Пусть существует непрерывная и непрерывно  дифференцируемая в D функция , являющаяся положительно определённой, причём . Тогда точка покоя  устойчива.

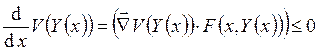Заметим, что последнее условие означает невозрастание функции  на траекториях системы. Действительно, если V рассматривается при , где  – решение системы , то . В этом случае говорят, что функция  не возрастает в силу системы .

Функция , обладающая свойствами, отмеченными в первой теореме Ляпунова называется функцией Ляпунова I-го рода.

Это значит, что точка покоя  устойчива, если существует функция Ляпунова I-го рода.

Вторая теорема Ляпунова: Пусть существует непрерывная и непрерывно дифференцируемая функция , причём , где  положительно определена в D. Тогда точка покоя  асимптотически устойчива.

Отметим, что выполнение последнего условия автоматически обеспечивает выполнение второго условия первой теоремы Ляпунова. Условие  означает, что  строго убывает.

Функция , обладающая свойствами, отмеченными во второй теореме Ляпунова называется функцией Ляпунова II-го рода.

Общих рекомендаций, позволяющих построить функцию Ляпунова II-го рода, нет.

Часто функция Ляпунова имеет прямое отношение к законам сохранения, например, функцией Ляпунова может оказаться функция энергии.