Рассмотрим систему
дифференциальных уравнений ![]() порядка
порядка ![]() . Предполагается, что
. Предполагается, что ![]() определена при
определена при ![]() и
и ![]() и что выполнены условия теоремы
существования и единственности решения. Будем полагать, что система
и что выполнены условия теоремы
существования и единственности решения. Будем полагать, что система ![]() имеет решение
имеет решение ![]() определённое
при
определённое
при ![]() .
.
Решение
![]() называется устойчивым (по Ляпунову), если
для
называется устойчивым (по Ляпунову), если
для ![]() при
при ![]() для
любого решения
для
любого решения ![]() , в начальный момент
, в начальный момент ![]() удовлетворяющего условию
удовлетворяющего условию ![]() .
.
Решение
![]() называется притягивающим при
называется притягивающим при ![]() , если
, если ![]() для
любого решения
для
любого решения ![]() .
.
Решение
![]() называется асимптотически устойчивым, если
оно устойчиво и является притягивающим.
называется асимптотически устойчивым, если
оно устойчиво и является притягивающим.
Решение
![]() , которое не является устойчивым, будем
называть неустойчивыми.
, которое не является устойчивым, будем
называть неустойчивыми.
Обычно исследование на
устойчивость произвольного решения ![]() сводят к исследованию
на устойчивость тривиального решения. В противном случае можно сделать замену
сводят к исследованию
на устойчивость тривиального решения. В противном случае можно сделать замену ![]() в уравнении
в уравнении ![]() .
Решению
.
Решению ![]() соответствует
соответствует ![]()
![]() . Т.к.
. Т.к. ![]() , то
, то ![]() , где
, где ![]()
![]() . Заметим, что
. Заметим, что ![]() .
.
Исследуем
на устойчивость ![]() в фазовом пространстве системы
в фазовом пространстве системы ![]() . Всякому постоянному решению отвечает
точка. Такие точки мы будем называть точками покоя системы
. Всякому постоянному решению отвечает
точка. Такие точки мы будем называть точками покоя системы ![]() .
.
Все предыдущие определения легко
переносятся в фазовые пространства. В этом случае можно говорить об устойчивых
точках покоя, асимптотически устойчивых точках покоя, неустойчивых точках
покоя. Если надо исследовать при ![]() , то можно сделать
замену
, то можно сделать
замену ![]() .
.
§5.2 Простейшие типы точек покоя на плоскости
Будем рассматривать систему 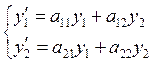 в векторной форме:
в векторной форме: 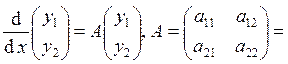
![]() . Точки покоя этой системы можно найти,
решая систему
. Точки покоя этой системы можно найти,
решая систему 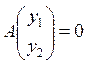 . Если
. Если ![]() ,
то эта система имеет единственное решение
,
то эта система имеет единственное решение ![]() , иначе
система имеет бесконечное множество решений. Ограничимся случаем
, иначе
система имеет бесконечное множество решений. Ограничимся случаем ![]() .
.
2.  Пусть
Пусть ![]() и
и ![]() –
собственные числа,
–
собственные числа, ![]() и
и ![]() –
соответствующие им собственные векторы. Общее решение системы представляется в
виде
–
соответствующие им собственные векторы. Общее решение системы представляется в
виде 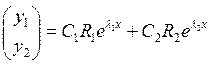 .
.
г)
![]() точка
покоя
точка
покоя ![]() асимптотически устойчива. Называется
устойчивым узлом.
асимптотически устойчива. Называется
устойчивым узлом.
д)
![]() .
Фазовый портрет подобен предыдущему, но направление движения противоположно.
Точка покоя
.
Фазовый портрет подобен предыдущему, но направление движения противоположно.
Точка покоя ![]() неустойчива
и называется неустойчивым узлом.
неустойчива
и называется неустойчивым узлом.
е)

![]() (второй
рисунок). Точка покоя
(второй
рисунок). Точка покоя ![]() является неустойчивой и
называется седлом.
является неустойчивой и
называется седлом.
3. Пусть A имеет комплексные собственные
числа: ![]() ,
, ![]() и
и ![]() – соответствующие им собственные векторы.
Тогда общее решение будет записываться в виде:
– соответствующие им собственные векторы.
Тогда общее решение будет записываться в виде: 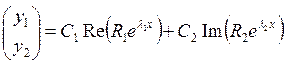 .
Удобнее записать его несколько иначе:
.
Удобнее записать его несколько иначе: 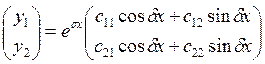 (здесь
(здесь
![]() – линейная комбинация
– линейная комбинация ![]() и
и ![]() ).
).
b)
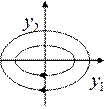
![]() Точка покоя
Точка покоя ![]() устойчива. Асимптотической устойчивости
нет. Точка покоя называется центром.
устойчива. Асимптотической устойчивости
нет. Точка покоя называется центром.
в) ![]() В первом
случае
В первом
случае ![]() точка покоя
точка покоя ![]() называется
устойчивым фокусом. Она асимптотически устойчива. Во втором случае
называется
устойчивым фокусом. Она асимптотически устойчива. Во втором случае ![]() точка покоя
точка покоя ![]() называется неустойчивым
фокусом.
называется неустойчивым
фокусом.
4. Матрица A имеет собственные значения ![]() , т.е.
собственное значение является кратным. Тогда оно вещественное.
, т.е.
собственное значение является кратным. Тогда оно вещественное.
в) Собственному
значению l соответствует два
линейно независимых вектора ![]() и
и ![]() . Общее решение:
. Общее решение: 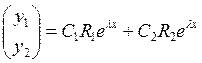 .
Все фазовые траектории прямолинейны. При
.
Все фазовые траектории прямолинейны. При ![]() точка покоя
точка покоя ![]() асимптотически
устойчива. Она называется устойчивым дикритическим узлом. При
асимптотически
устойчива. Она называется устойчивым дикритическим узлом. При ![]() точка покоя
точка покоя ![]() неустойчива.
Она называется неустойчивым дикритическим узлом.
неустойчива.
Она называется неустойчивым дикритическим узлом.
г)  Собственному
значению l соответствует один
линейно независимый вектор
Собственному
значению l соответствует один
линейно независимый вектор ![]() . Общее решение:
. Общее решение: 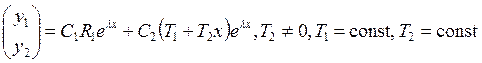 . Можно считать, что
. Можно считать, что ![]() . Здесь при
. Здесь при ![]() точка покоя
точка покоя ![]() асимптотически
устойчива. Она называется устойчивым (вырожденным) узлом. При
асимптотически
устойчива. Она называется устойчивым (вырожденным) узлом. При ![]() точка покоя
точка покоя ![]() неустойчива.
Она называется неустойчивым (вырожденным) узлом.
неустойчива.
Она называется неустойчивым (вырожденным) узлом.
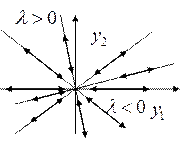 Эта картина получается из
первого случая
Эта картина получается из
первого случая ![]() при
при ![]() .
.
Отметим, что из условия ![]() следует, что матрица A
не имеет нулевых собственных значений. Однако можно рассмотреть аналогичными
методами и случай вырожденной матрицы A.
следует, что матрица A
не имеет нулевых собственных значений. Однако можно рассмотреть аналогичными
методами и случай вырожденной матрицы A.
 Проведённый анализ позволяет
утверждать следующее:
Проведённый анализ позволяет
утверждать следующее:
3. Если все
собственные значения матрицы имеют отрицательную вещественную часть, то точка
покоя ![]() асимптотически устойчива (устойчивые узлы
и фокусы).
асимптотически устойчива (устойчивые узлы
и фокусы).
4. Если хотя
бы одно собственное значение матрицы имеет отрицательную вещественную часть, то
точка покоя ![]() неустойчива (неустойчивые узлы, сёдла).
неустойчива (неустойчивые узлы, сёдла).
Во втором случае второе собственное значение может быть нулевым. В остальных случаях требуется дополнительное условие.
Приведённые утверждения остаются справедливыми, если порядок системы равен n.
§5.3 Исследование на устойчивость по первому приближению
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.