Основные понятия теории дифференциальных уравнений. Уравнения первого порядка. Устойчивость решений дифференциальных уравнений. Уравнения с частными производными первого порядка, страница 11

4.  Параметризация. Интегральные линия уравнения описываются в параметрическом виде. В простейших случаях можно обойтись одним параметром: . Так решаются, например, уравнение Клеро  и уравнение Лагранжа .

Для уравнений, неразрешённых относительно производной также можно ввести понятие особой точки, особого решения.

Глава 2. Уравнения порядка выше первого.

§ 2.1 Теорема о существовании и единственности решения задачи Коши.

В общем случае уравнения порядка выше первого представляются в виде . Если такое уравнение приводится к виду , то оно называется уравнением, разрешённым относительно старшей производной. Будем полагать, что f определена в области . Зафиксируем . Дополнив уравнение начальными условиями:   получим задачу Коши.

Пусть функция f непрерывна в D и имеет в D непрерывные производные по всем аргументам, начиная со второго. Тогда найдётся отрезок , на котором задача Коши имеет единственное решение.

При условиях теоремы общее решение уравнения  представляется в виде , где  – произвольные постоянные.

Для доказательства теоремы часто уравнение  сводят к системе уравнений. Вводятся новые переменные: . В результате получается система: . Начальные условия при этом принимают вид: . Таким образом, задача Коши сопоставляется с другой задачей Коши, составленной из новых переменных. Свойства системы подобны свойствам уравнения, разрешённого относительно производной из предыдущего раздела. Поэтому она может быть исследована прежними методами. Решив эту задачу Коши, выберем компоненту  и получим решение старой задачи Коши.

Отметим, что под решением уравнения  понимается функция непрерывная и имеющая непрерывные производные до порядка n включительно, которая, будучи подставленной в уравнение обращает его в тождество.

§ 2.2 Линейные уравнения. Общие свойства линейных уравнений.

Под линейными уравнением будем понимать уравнение вида . Здесь  – коэффициенты уравнения. Если , то уравнение называется уравнением с переменными коэффициентами. Если  постоянны, то уравнение называется уравнением с постоянными коэффициентами. Функция  – неоднородность уравнения. Если , то уравнение называется однородным. В противном случае – неоднородным. Если в неоднородном уравнении формально отбросить , то получится соответствующее однородное уравнение.

Введём формальный оператор . Тогда уравнение примет вид: .

Общие свойства линейных уравнений:

4.  Пусть  – решение . Тогда  – решение этого же уравнения при .

5.  Пусть  и  – решения уравнения . Тогда  – решение .

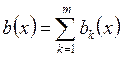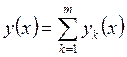6.  (принцип суперпозиции) Пусть в уравнении  неоднородность  представляется в виде: . Пусть  – решение уравнения . Тогда  – решение .

Пусть  – решения однородного уравнения. Тогда 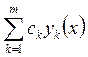 – решение этого же уравнения при .

Пусть  – решение уравнения  – решение . Тогда  – решение уравнения .

Следствия дают программу дальнейших исследований. Первое следствие приведёт к общему решению однородного уравнения, а второе – к общему решению неоднородного уравнения.

Пусть уравнение  с вещественными коэффициентами имеет комплексное решение . Тогда  и  – вещественные решения этого же уравнения.

В дальнейшем будем полагать, что функции  и  определены на .

Пусть . Дополним уравнение  начальными условиями , где  – заданные значения. Получим задачу Коши.

Пусть функции  непрерывны на . Тогда задача Коши имеет единственное решение на всём .

Далее считаем, что  – непрерывны на .

§ 2.3 Решение однородных линейных уравнений

Пусть на  рассматриваются функции . Эти функции называются линейно независимыми на , если линейная комбинация  с постоянными  только при , иначе – линейно зависимыми.

Теорема о линейно зависимых функциях: Пусть функции  линейно зависимы на , непрерывны и имеют непрерывные производные до порядка . Тогда 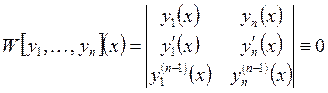 (определитель Вронского).

Функции  по условию линейно зависимы, т.е. , для которых 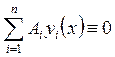 на . Тогда 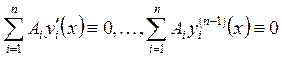. Имеем систему тождеств. При каждом фиксированном x эту систему можно рассматривать как систему уравнений относительно . Это линейно однородная система, имеющая нетривиальные решения, следовательно, матрица системы вырожденная и её определитель .