Механизмы с постоянной нагрузкой. Расчётные схемы механической части ЭП. Понятие многомассовой механической системы. Регулируемый ЭП с обратной связью по скорости и по току якоря. Силовые преобразователи переменного тока, страница 8

Обмотка возбуждения создает основной рабочий магнитный поток. При  практически не приводит к увеличению Ф. При необходимости изменения Ф его можно только уменьшать.

24. Математическая модель ДПТНВ

Мат модель может быть получена из анализа обобщенной электрической машины. Но для ДПТНВ ввиду очевидности физических процессов ее можно получить непосредственно. В уравнение войдут:

1)  Уравнение электрического равновесия цепи якоря

2)  Уравнение электрического равновесия цепи возбуждения

3)  Уравнение электро-механической связи

4)  Уравнение движения (связь ЭД с механизмом)

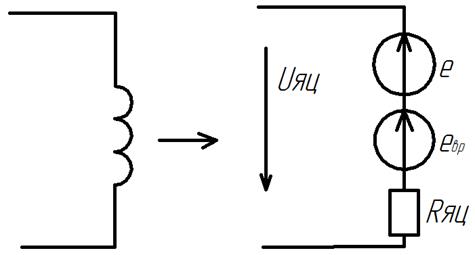
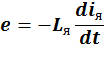
1)   – Электрическая цепь. e – ЭДС самоиндукции, возникающая в переходных процессах при изменении i_я

2) 

3) 

4) 

Эти 4 уравнения – Система (1)

Влияние на электрическую цепь реализуется через ЭДС вращения:

 - активное сопротивление якорной цепи.

 - полная индуктивность якорной цепи

 – конструктивный коэффициент двигателя.

 - число пар полюсов

N – число активных проводников якоря, участвующих в создании момента

a – число параллельных ветвей обмотки якоря

Ф – магнитный поток возбуждения

 - Индуктивность обмотки возбуждения

М – электро-магнитный момент двигателя

Mc – момент сопротивления нагрузки

J – момент инерции привода

При расчетах K и Ф отдельно не используются, а применяется их произведение ,     . Его находят из формулы статического равновесия цепи якоря.                                  ,                      

Алгебраизируя систему (1) и вводя обозначения ,  [c] имеем:

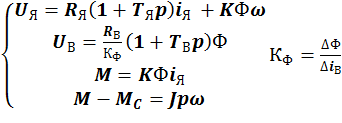
24. Структурная схема ДПТНВ

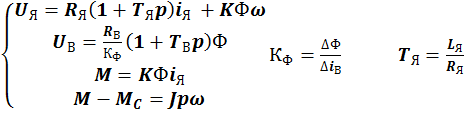,  [c]

По данным уравнениям можно составить структурную схему:

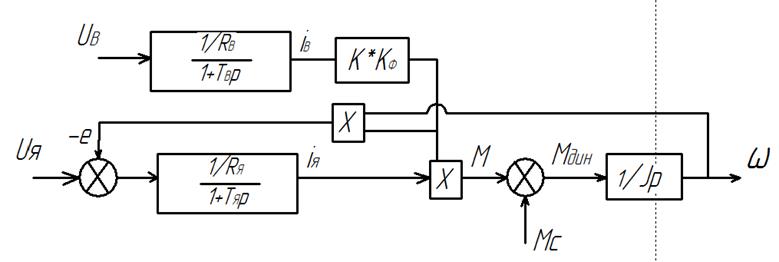
Имеем 2 канала управления:

1)  Потоком

2) 

Канал управления полем содержит апериодическое звено с постоянной времени.

 - на линейной части. Обычно  в пределах 0.2-5 с, 0.2 – для больших мощностей, 5 с – для малых мощностей. Анализ структурной схемы показывает, что при изменении потока математическое описание нелинейно, т.к. содержит произведение переменных величин и для анализа требуется ЭВМ. При номинальном потоке и постоянном токе, что характерно для ДПТНВ система упрощается. Уравнение механической характеристики в этом режиме имеет вид:

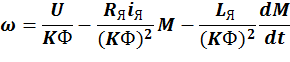
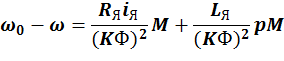
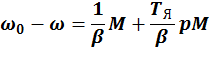
Получили уравнение динамической механической характеристики. Можно обратить внимание, что в динамике постоянная времени, т.е. инерционность якорной цепи возрастает.

25. Динамическая модель ДПТНВ

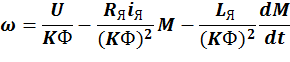
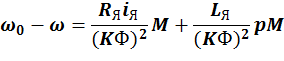
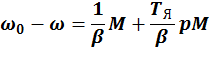
Получили уравнение динамической механической характеристики. Можно обратить внимание, что в динамике постоянная времени, т.е. инерционность якорной цепи возрастает.

Структурная схема имеет вид:

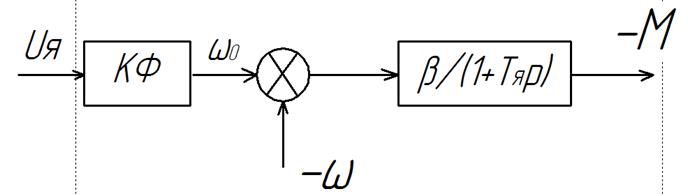
Если модель рассматривать как управляющее воздействие для механической системы, то ДПТНВ при постоянном потоке представляет собой апериодическое звено с постоянной времени.  может быть рассчитана по приближенной формуле:

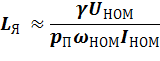
   для некомпенсированных ЭД

 для компенсированных ЭД

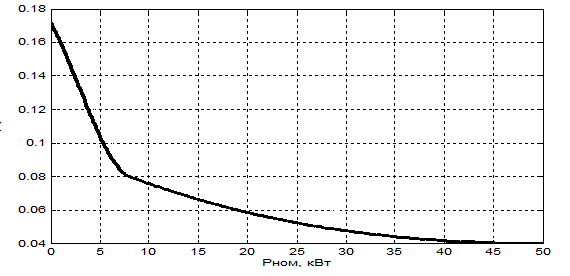
Обычно . Значение  может приводиться в каталогах, если их нет, то приблизительно можно определить по универсальной кривой

,   

Можно  приблизительно оценить, считая что половина номинальных потерь приходится на якорь:

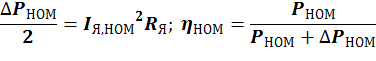
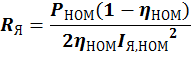
Уравнение динамической характеристики устанавливает связь между скоростью и моментом для любых режимов работы. Форма конкретной механической характеристики зависит от различных факторов:

1)  Вида механической системы (есть ли упругость, воздушные зазоры)

2)  Начальных условий (стоял или вращался)

3)  Управляющих и возмущающих воздействий

26. Частотный анализ ДПТНВ

1)   – Электрическая цепь. e – ЭДС самоиндукции, возникающая в переходных процессах при изменении i_я

2) 

3) 

4) 

Решая эту систему относительно  при   и постоянном моменте сопротивления имеем:

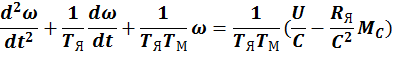
Решая относительно момента при тех же условиях имеем:

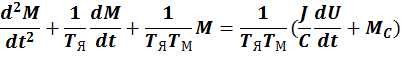
Здесь  - скорость холостого хода

 – изменение скорости, вызванное падением напряжения на  от тока нагрузки

 - динамическая составляемая момента, развиваемая двигателем, вызванная изменением питающего якоря напряжения.

 – электро-магнитная постоянная времени

Алгебраизируя имеем:

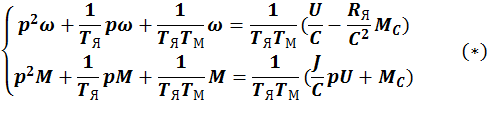
Передаточная функция ДПТНВ при возмущении по управлению: