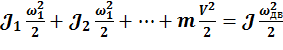Механизмы с постоянной нагрузкой. Расчётные схемы механической части ЭП. Понятие многомассовой механической системы. Регулируемый ЭП с обратной связью по скорости и по току якоря. Силовые преобразователи переменного тока, страница 4

+ где - момент инерции ротора двигателя, а -- соответствующие механические части:

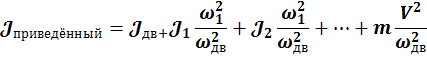
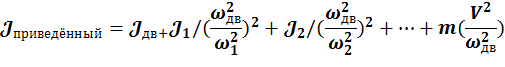
Пусть , тогда 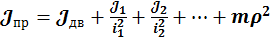, где  – радиус приведения, i1- передаточное число.

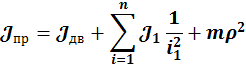
В каталогах вместо иногда приводят маховый момент , тогда в системе СИ . При приведении   учитывать потери при передаче не следует.

Для практических расчётов при вращательном движении приближённо:

, где - в справочнике, σ – 1.1 – 1.3(механизмы подъёма, передвижения кранов); 1.25 – 1.4(механизмы непрерывного транспорта, компрессоры, работают через редуктор с I < 25)

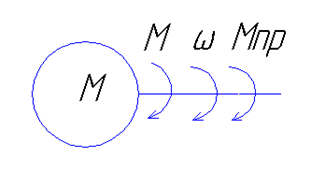
Если имеется и поступательное движение то

8.8Приведение момента сопротивления

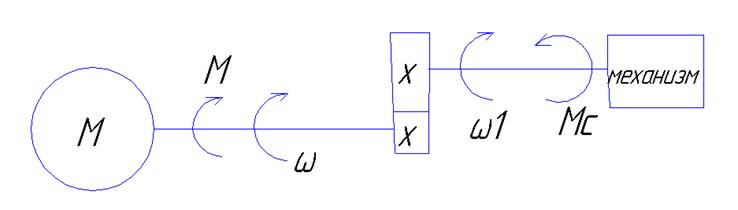
Необходимо привести (пересчитать) Мс на вал двигателя , так мощность должна оставаться неизменной реальной и приведённых схем.

          

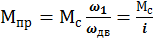
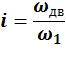
Если движение поступательное:

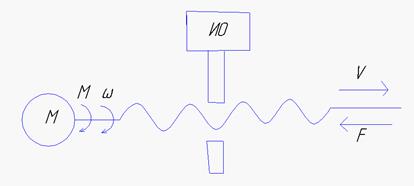
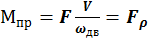 ,  , где φ – угол  поворота

Потери в механических передачах в реальных механизмах равенством мощности на приводимых валах нарушаются.

Мощность на валу двигателя или сопротивления будет больше на величину потерь и на трение в передачах, т.е.

Если известно КПД передачи то потери на трение могут быть учтены путём увеличения приведённого момента:, где η – КПД.

При поступательном:

Иногда возникает необходимость выделить из привидённого момента усилие(момент) затрачиваемый на преодоление сопротивления трения:

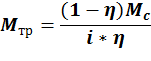
Обычно КПД механической передачи со скоростью. Можно учесть это изменение по средствам коэфициета β:

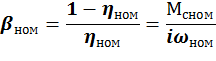
Более точно β находится экспериментально.

8.10.Приведениие жесткости механической передачи

При приведении должна сохраняться потенциальная энергия деформации в приведённой и реальной схемах.

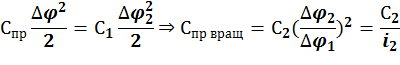
11.Понятие многомассовой механической системы

При проектировании и исследовании ЭП моменты инерции, массы, упругости связи реальных элементов обычно известны. Действующие системы сил(моменты) либо заданны, либо расчитываются по исходным данным механизма и технологии. После приведения их к расчётной скорости(вала двигателя) можно выбрать главные массы (инерционные) и главные упругие связи. Несущественные можно отбросить и на их основе составить приближённую расчётную схему механической части. Исследование динамики ЭП показывает что в большинстве случаев механические системы сводятся к 3-х, 2-ч и одномассовой расчётной схеме.

3-х массовая механическая система

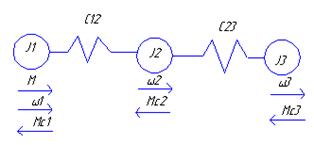J1—совокупные приведённые массы эл-тов связи м-ду которыми жёсткие;

J2,J3—аналогично; С23, С12 – эквиволентные жёсткости мех. упругих связей м-ду массами: 1-я масса представляет ротор двигателя и жёстко связанные с им элементы. К этой массе приложены электромагнитный момент М и момент статической нагрузки Мс1, который обычно является моментом потерь на валу двигателя и жёстко связанным с ним эл-том. К промежуточной массе J2 приложен момент сопротивления Мс2(обычно вызванный потерями м-ду упругостями), а к третьей приложен момент Мс3(момент нагрузки).

3-х массовая упругая система используется в случаях достаточно детального анализа условий движения масс механизма.

2-х массовая модель:

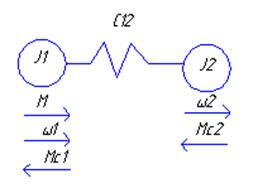
Мс2—нагрузка; J1 – ротор+ жёстко связанные с ним элементы, J2 – механизм и жёстко связанные с ним элементы.

Двухмассовая модель более простая модель ЭП учитывающая упругие связи и является основной при исследовании ЭП.

Одномассовая модель:

В случаях когда влияние незначительно используют одномассовую модель – жёсткое привидённое звено. В этом случае многомассовая механическая часть ЭП заменяется одной эквиволентной массой с моментом инерции , на которую воздействуют Мдв и суммарный момент нагрузки(технология+трение) приведённые к валу двигателя: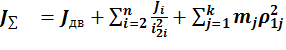, где n и k – число масссовершающих вращательное и поступательное движение. Суммарный приведённый к валу двигателя момент статической нагрузки Мс:

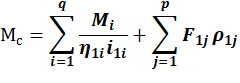
12Механическая часть Э.П. как объекта управления (на примере 2-х массовой системы)

Структуру и математическую модель системы можно составить исходя из очевидных физических соображений. В случаях, когда математическая модель и структура не очевидна, ее можно получить из формулы Лагранжа. Уравнение движения позволяет проанализировать динамич. особенности Э.П. механической части как объекта управления. Математическая модель и на ее основе составленная структурная схема являются основой для анализа объекта.