Механизмы с постоянной нагрузкой. Расчётные схемы механической части ЭП. Понятие многомассовой механической системы. Регулируемый ЭП с обратной связью по скорости и по току якоря. Силовые преобразователи переменного тока, страница 13

Направление тока якоря I_я и ЭДС Е рис.2.9, 2.10 показано для двигательного режима.

Напряжение U_я (В), приложенное к якорю, в установившемся режиме уравновешивается ЭДС Е (В), наведенной в якоре (ее называют также противоЭДС), и падением напряжения в якорной цепи

       U_я = Е + I_я(R_я+R_д),                                                        (2.12)

где R_я – сопротивление якорной цепи двигателя, Ом, включающее сопротивления обмотки якоря, щеточного контакта, дополнительных полюсов и компенсационной обмотки; R_д – добавочное сопротивление.

ЭДС машины определяется соотношением

                                            Е= сФw_д,                                                              (2.13)

здесь конструктивный коэффициент

с = рN/ 2pа,

р – число пар полюсов;

N – число активных проводников обмотки якоря;

а – число пар параллельных ветвей обмотки якоря;

Ф – магнитный поток, Вб, создаваемый обмоткой возбуждения или постоянными магнитами.

Подставляя выражение (2.13) для Е в уравнение (2.12) и решая его относительно w_д, получим:

w_д = .                                       (2.14)

Это уравнение устанавливает связь между частотой вращения и током якоря w_д = f(Iя) и называется электромеханической характеристикой двигателя.

Электромагнитный момент двигателя (Н×м), определяется током якоря и магнитным потоком:

                                           М = сФI_я.                                                              (2.15)

Момент на валу двигателя меньше электромагнитного на значение, определяемое потерями в стали и механическими потерями. Для инженерных расчетов этими потерями можно пренебречь, и принять, что момент на валу равен электромагнитному моменту. Тогда, определив из (2.15) ток якоря и подставив его в соотношение (2.14), получим уравнение механической характеристики двигателя:

w_д = .                                       (2.16)

Полученные выражения (2.14), (2.16) для характеристик двигателя представляют собой уравнение прямой. Они справедливы, если пренебречь реакцией якоря.

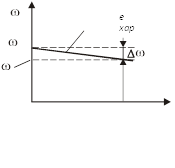
В уравнениях (2.14), (2.16) первое слагаемое представляет собой угловую скорость идеального холостого хода (при этом ток якоря и момент равны 0)

w₀ = .                                              (2.17)

Второй член в этих уравнениях характеризует статическое падение угловой скорости от нагрузки

         или                      (2.18)

29-2

На рис. 2.11 падение скорости показано для номинального значения момента M_ном(тока I_ном). При неизменном магнитном потоке момент и ток якоря, как следует из соотношения (2.15) пропорциональны. Поэтому механическая и электромеханическая характеристики двигателя (см. рис. 2.11) отличаются только масштабом по оси ординат. Характеристика, полученная при номинальном значении напряжения на якоре U_ном, номинальном магнитном потоке Ф_ном и

отсутствие внешних резисторов в якорной цепи, называется естественной. Жесткость естественной характеристики определяется только сопротивлением якорной цепи двигателя:

  или .                                   (2.19)

Снижение скорости w_д под нагрузкой объясняется следующим. При увеличении момента сопротивления механизма угловая скорость начинает снижаться. В результате уменьшается ЭДС Е согласно (2.13). Ток якоря при этом, как следует из (2.12) увеличивается. Соответственно возрастает момент двигателя (см. уравнение (2.15)). Этот процесс продолжается до тех пор, пока момент двигателя не сравняется с моментом сопротивления. После достижения равенства М=М_с наступит новый установившийся режим с меньшей угловой скоростью w_д.

При инженерных расчетах коэффициенты, входящие в уравнения характеристик двигателя, могут быть определены через номинальные параметры двигателя, приводимые в каталогах. При номинальном магнитном потоке

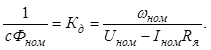                                      (2.20)

Здесь коэффициент К_д - коэффициент передачи двигателя, его размерность . С использованием этого понятия уравнения (2.14), (2.16) могут быть переписаны в виде:

                                 (2.21)

                                 (2.22)