Из б) видно что при ![]() →∞ (высокие частоты) на характер процесса
также влияет только интегрирующее звено.
→∞ (высокие частоты) на характер процесса
также влияет только интегрирующее звено.
Вывод: при синтезе ЭП если J1 во много раз
меньше J2 или ![]() во много раз больше частоты среза
во много раз больше частоты среза ![]() , где
, где ![]() --
частота среза желаемой ЛАЧХ разомкнутого контура регулирования; мех часть ЭП
можно представить жёстким механическим звеном и не учитывать влияние упругости.
--
частота среза желаемой ЛАЧХ разомкнутого контура регулирования; мех часть ЭП
можно представить жёстким механическим звеном и не учитывать влияние упругости.
Анализ рисунка Б и формула а) показывают что колебательность 2-ой массы выше чем первой. В низкочастотной области движение определяется также интегрирующим звеном.
Сочетание параметров ЭП когда J2 во много раз
меньше J1 или ![]() →∞ достаточно распространены. Поэтому часто
ЭП представляют в виде жёсткого приведённого звена у которого частотные
характеристики не отличаются от низкочастотных характеристик предыдущего
варианта.
→∞ достаточно распространены. Поэтому часто
ЭП представляют в виде жёсткого приведённого звена у которого частотные
характеристики не отличаются от низкочастотных характеристик предыдущего
варианта.
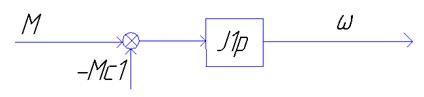
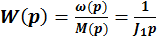
АФХ:р→∞
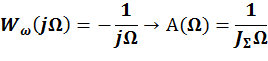
![]() =const
=const
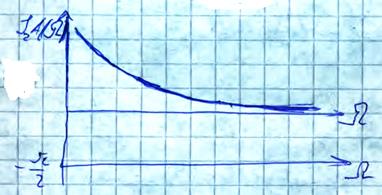
При ![]() амплитуда скорости неограниченно возрастает к ∞.
Физическое объяснение: при Мдин=const статически установившийся процесс
наступает при скорости
амплитуда скорости неограниченно возрастает к ∞.
Физическое объяснение: при Мдин=const статически установившийся процесс
наступает при скорости ![]() , т.к. при этом
, т.к. при этом ![]()
Если Мдин изменяется с частотой ![]() то амплитуда колебаний скорости ограничивается
механической инерцией. Тем в большей степени ограничение чем больше частота.
то амплитуда колебаний скорости ограничивается
механической инерцией. Тем в большей степени ограничение чем больше частота.
Т.к. убывание амплитуд с ростом частоты происходит достаточно быстро то при частоте 30-60 Гц и ограниченных по величине Мдин – колебаниями скорости обычно пренебрегают.
Вывод: в следствии инерции механическая часть ЭП является ФНЧ
16. Механ перех процессы(МПП) Мдин=const, w,φ,tпп=?
Изменение упр-щего или возмущ-го возд-вия вызывает в динамич системе ПП. В этом случае М≠Мс, возникает Мдин=М-Мс. Хар-р ПП опред-ся з-ном изменения Мдин. Рассмотрение МПП для опред-ния ω(t),φ(t), иногда tпп, ε(t). Предполаг-ся изветным М(t) и Mc(t).Мдин=const –такой процесс возник когда мех хар-ки двиг-ля и механ-ма паралл-ны.
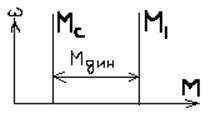
Искомые координаты получ-ся решением основного
ур-ния движ-ния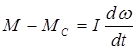 , ситают что I=const.
, ситают что I=const.
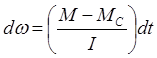 . M-Mc=const
(по условию). Интегрируя:
. M-Mc=const
(по условию). Интегрируя: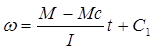 . С1 наход
из н.у. (tН=0):
С1=ωНАЧ.
. С1 наход
из н.у. (tН=0):
С1=ωНАЧ. 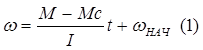
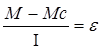 . Если М>Мс, то имеем
. Если М>Мс, то имеем 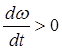 , т.е. ускорение с “+”(разгон). Если
М<Мс, ускор-ние с “-”(торм-ние).
, т.е. ускорение с “+”(разгон). Если
М<Мс, ускор-ние с “-”(торм-ние).
tпп=? 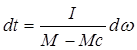 , подставим в 1
исследуемое tпп получ:
, подставим в 1
исследуемое tпп получ:
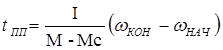 . Если мех-изм связан с
перемещ-ем φ(t):
. Если мех-изм связан с
перемещ-ем φ(t): ![]() Подставляем в (1) последнее выраж:
Подставляем в (1) последнее выраж: 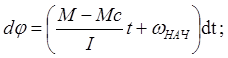
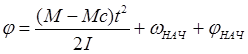
 Полученные рез-ты
часто исп-т при выполнении различн расчетов. В ЭП при рассмотр ПП.
Полученные рез-ты
часто исп-т при выполнении различн расчетов. В ЭП при рассмотр ПП.
17.Механ перех процес (МПП) при лин-ых завис-тях M(w) двиг-ля и Mc(w).
Изменение упр-щего или возмущ-го возд-вия вызывает в динамич системе ПП. В этом случае М≠Мс, возникает Мдин=М-Мс. Хар-р ПП опред-ся з-ном изменения Мдин. Рассмотрение МПП для опред-ния ω(t),φ(t), иногда tпп, ε(t). Предполаг-ся изветным М(t) и Mc(t).Случай распростр-ный для АД (раб часть мех-кой хар-ки линейна) и ДТП НВ.
Мех хар-ка: 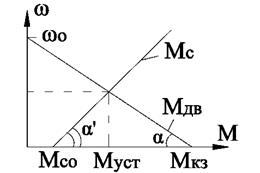
Из постановки вытекает, что Мдин также лин-но зав-т
от скор-ти. Опишем хар-ки Ур-ниями. Для Мдв: y=N+kX.
Введем понятие жесткости мех хар-ки: 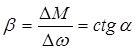
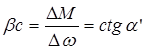
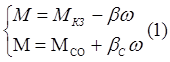
Мкз, Мсо – моменты двиг-ля и мех-ма при нулевой скор-ти. Найдем w,φ,tпп=?
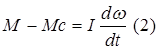 . Подставим (1) в (2)
получим:
. Подставим (1) в (2)
получим: 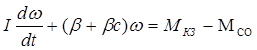
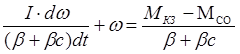 . Обозначим
. Обозначим 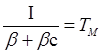 .
.
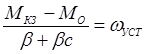
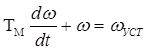 . Решение вида:
. Решение вида: ![]() . Из
н.у. при t=0 имеем A=ωНАЧ-ωУСТ.
. Из
н.у. при t=0 имеем A=ωНАЧ-ωУСТ.
![]()
 З-н изменения момента двиг-ля от
ф-ции времени.
З-н изменения момента двиг-ля от
ф-ции времени. ![]() . Учитывая, что
. Учитывая, что 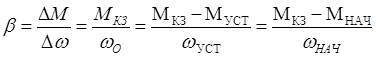 . Получим после подстановки ωНАЧ
и ωУСТ з-ны изменения:
. Получим после подстановки ωНАЧ
и ωУСТ з-ны изменения:![]() . Время ПП (tпп),
за котор измен-ся ω от ωНАЧ до ωКОН или момент от МНАЧ
до МКОН. Опред-ся из ф-ции ω(t)
путем логарифм-ния.
. Время ПП (tпп),
за котор измен-ся ω от ωНАЧ до ωКОН или момент от МНАЧ
до МКОН. Опред-ся из ф-ции ω(t)
путем логарифм-ния. 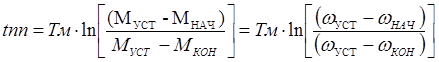 . Примечание: для распростр-го
случая, когда βс=0 (жесткость нулевая, хар-ка пар-на оси скор-тей) пар-ры
упрощаются и приним вид:
. Примечание: для распростр-го
случая, когда βс=0 (жесткость нулевая, хар-ка пар-на оси скор-тей) пар-ры
упрощаются и приним вид: 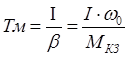
![]() . Анализ: скор-ть ω и момент М измен-ся во
времени в соотв-вии с exp
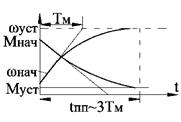
ф-цией характер-мой пост времени Тм:
. Анализ: скор-ть ω и момент М измен-ся во
времени в соотв-вии с exp
ф-цией характер-мой пост времени Тм:
18. ПП мех-кой системы при экспоненциальном моменте двигателя и Мс=const.
Изменение упр-щего или возмущ-го возд-вия вызывает в динамич системе ПП. В этом случае М≠Мс, возникает Мдин=М-Мс. Хар-р ПП опред-ся з-ном изменения Мдин. Рассмотрение МПП для опред-ния ω(t),φ(t), иногда tпп, ε(t). Предполаг-ся изветным М(t) и Mc(t).Пусть ωНАЧ=0 (пуск), а к ротору приклад-ся эл-магн момент, изменяющийся по з-ну:
![]()
Ур-ние движ-ния: 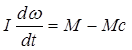 ;
; 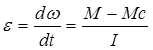
![]()
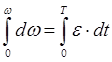
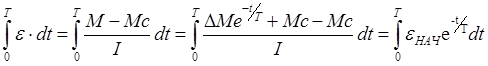
![]() εНАЧ – нач
ускорение.
εНАЧ – нач
ускорение. 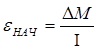
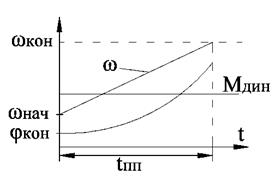
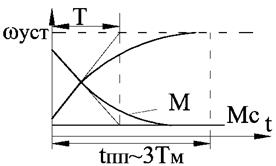
График: ω нарастает по exp-ной зав-ти от 0 до ωУСТ, где ωУСТ= εНАЧТ, с ускорением уменьшающимся по мере возраст ω, тк уменьш-ся Mдин=М-Мс.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.