Механизмы с постоянной нагрузкой. Расчётные схемы механической части ЭП. Понятие многомассовой механической системы. Регулируемый ЭП с обратной связью по скорости и по току якоря. Силовые преобразователи переменного тока, страница 5

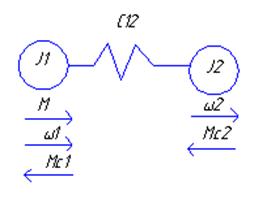
На основании схемы можно получить уравнение:

M -- =  = (p = ) = p

- = , = p

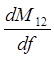= (-), где  = , =

Где

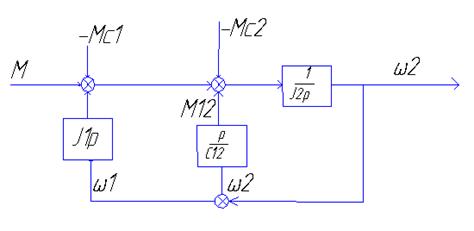
Полученная схема – математическая модель двухмассовой упругой с-мы. На основании уравнений можно составить структурную схему.

Полученная схема – математическая модель двухмассовой упругой с-мы. На основании уравнений можно составить структурную схему.

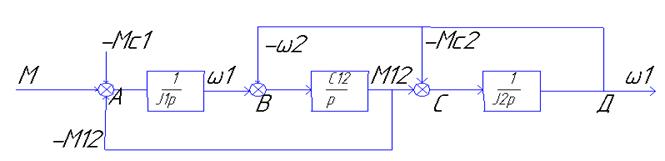Состоит из 3-х интегрир. звеньев вида . Управл. воздействием является М. Возмущаемыми: , . Регулируемыми переменными могут быть , , перемещение  и , момент упругого взаимодействия . Преобразуем структурную схему. Найдем передаточную функцию по управлению при координате , а далее . При этом считаем, что  и равны нулю. Преобразуем структурную схему: для этого перенесем внутреннюю связь по упругому моменту на выход с-мы (т. С в т. D).

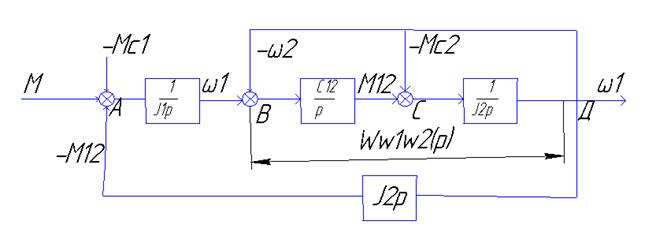
Определяем = = =

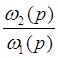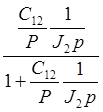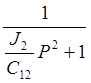
Определим = = 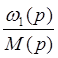(прямого канала)

Передаточная функция обр. связи при :  = (p) × 

(контура) = = =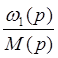

= = =

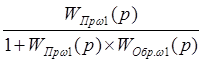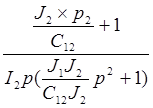
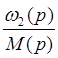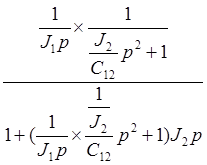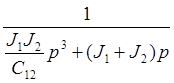
ХАУ: 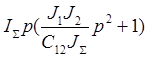= 0

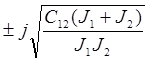= 0; = = , Где - резонансная частота (частота свободных колебаний) двухмассовой упругой с-мы.

13.Двухмассовая упругая с-ма представляет собой колебательное звено. - частота свободных колебаний и на этой частоте возможно появление мех. резонанса.

Очевидно, что полученный вид структурной схемы не единственный. Решив уравнения математической модели относительно (1-е уравнение в с-ме), а 3-е относительно , получим структурную схему:

В результате анализа получим закон изменения второй массы .

Если входами считать М,  и , а выходами , получим структурную схему, позволяющую анализировать  упругих сил.

1)  = М, = ; 2) = М,  = ; 3)  = ,=   

Продолжим анализ первой схемы.

Рассмотрим подробнее движение 1-ой массы. Для удобства обозначим  = 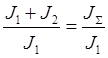- соотношение масс.

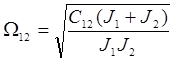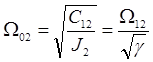; - резонансная частота второй массы.

- (собственные колебания второй массы при жесткой заделке первой, то есть )

Тогда =

=

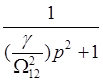
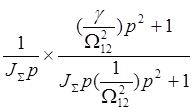
Тогда мех. часть Э.П. можно представить в виде 3-х звеньев:

Тогда передаточная функция = = 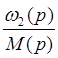×=  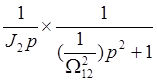(а)

14. Для анализа используем частотный метод. Для этого заменим p на . Тогда движение первой массы:

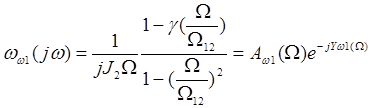(б)

где , а

Асимптотическая ЛАЧХ могут быть построены по передаточной функции =  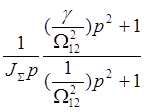, которую логично представить последовательным соединением интегрирующего звена, формирующего звена 2-го порядка с частотой сопряжения 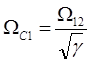 и идеального колебательного звена с резонансной частотой: .

При передаточная функция , так как числитель = 0.

log 0 = - и ЛАЧХ  -(1-ый разрыв).

При  имеет место полюс передаточной функции, и амплитуда стремится к +, образуя второй разрыв.

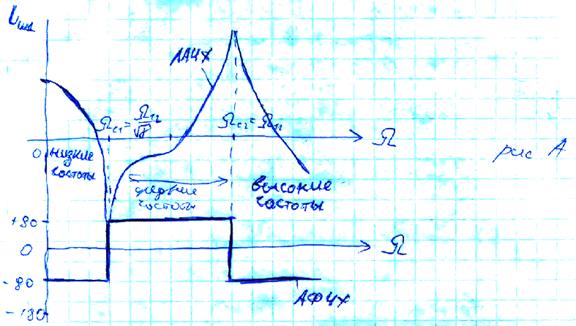
Анализ ЛАЧХ при  (уравнение б) определяется интегрирующим звеном и составляет -90º. При  (частота среза) скачком меняет знак числитель (уравнение б), что соответствует уменьшению фазового сдвига на 180º. Затем на частоте  изменяется знак и знаменателя и фазовый сдвиг опят возвращается к -90º.

Построим ЛФЧХ скорости :

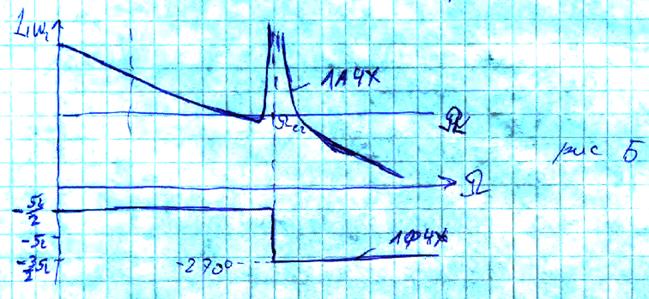
ЛАЧХ и ЛФЧХ при построили на основании уравнения а. В этом уравнении числитель =1 и не меняет знак на всех частотах. Разрыв ЛАЧХ происходит только на частоте . ЛФЧХ на этой частоте изменяет фазу на «-270º», сохраняя при этом знак (фазовый сдвиг между колебаниями момента и скорости).

Указанные характеристики показывают влияние упругости на движение 1-ой и 2-ой массы.

Движение первой массы при низких частотах колебаний управляющего воздействия М (см. рисунок «а» и формулу «б») определяется суммарным моментом  Э.П. Причем мех. часть ведет себя как интегрирующее звено. Так, при  изменяется по линейному закону на который накладываются колебания, обусловленные колебаниями упругой связи. Интегрирующее звено характериз. условия движения динамической системы в среднем.  При приближении ч-ты колебаний управляющего  момента к резонансной  амплитуда колебаний скорости (рис.Б) стремится к бесконечности. На появление резонанса влияют параметры механической части(присутствие форсирующего звена 2-го порядка). Можно выявить условия при которых влияние упругости на будет незначительным. Так из ур-я а) следует что J1 во много раз меньше J2, т.е. →1, а J2 незначительно, то движение определяется интегрирующим звеном .