Передача энергии турбинному колесу и создание на нём
вращающего момента возможны, если масло при взаимодействии с лопатками этого
колеса теряет часть своей абсолютной скорости, т.е. если u2н
>u1т. Это
происходит, если u1т<u2н,
т.е. при wт<
wн.
Чем больше разности скоростей 
и 
, тем больше сила давления масла на лопатки
турбины и тем больше вращающий момент.
При уменьшении нагрузки на турбинном колесе его скорость увеличивается. В случае нулевой нагрузки турбинное и насосное колёса вращаются с одинаковой скоростью, масло с лопаток насосного на лопатки турбинного колеса не переходит.
Необходимым условием передачи вращающего момента гидромуфтойявляется отставание турбинного колеса от насосного, т.е.wт<wн.Если турбинное колесо остановить (застопорить) внешней нагрузкой, то вращающий момент на нём достигнет максимального значения.
Поскольку в замкнутом пространстве гидромуфты взаимодействуют через масло два тела (два колеса), то очевидно, что вращающие моменты на насосном и турбинном колесах одинаковы (Тн = Тт ).
Итак, характерные особенности работы гидромуфты:
- вращающий момент на турбинном колесе создаётся, если скорость wт турбинного колеса меньше скорости wн насосного;
- вращающий момент на турбинном колесе достигает максимума при wт= 0;
- вращающие моменты на колёсах одинаковы ( Тн = Тт).
Гидродинамическая муфта асинхронна – скорости ведущего (насосного) и ведомого (турбинного) колёс различны. Скорость ведомого колеса автоматически уменьшается с увеличением нагрузки и наоборот.
Передаточное отношение.Поскольку гидромуфта асинхронна, для неё применимо понятие передаточное отношение. Традиционно в механике передаточное отношение определяют как отношение скорости ведущего звена к скорости ведомого. Для гидромуфт, у которых ведомое звено может иметь нулевую скорость, принято определять передаточное как отношение скорости ведомого звена к скорости ведущего. Передаточное отношение гидромуфты:
i = ωт/ωн. (14.1)
Величина i изменяется от нуля (турбина остановлена вследствие перегрузки, wт = 0) до единицы (на турбине нет нагрузки, wт = wн), т.е. 0 £i£1.
КПД гидромуфты:
,
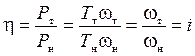(14.2)
где РТ – мощность на валу турбинного колеса; Рн – мощность на валу насосного колеса.
Ниже будет показано, что равенство η = 1 справедливо при 0 ≤ i ≤ 0,95.
Вращающий момент на насосном колесе.
Как показано в главе 13, вращающий момент Тн на колесе
лопастного насоса пропорционален величине комплекса 
. В
качестве безразмерного коэффициента пропорциональности принят коэффициент
вращающего момента l:
, (14.3)
где D2н — наибольший диаметр насосного колеса гидромуфты.
Величина λ зависит от нагрузки на турбинном колесе Тт и передаточного отношения i. Максимальное значение величины l бывает при wт = 0 и находится в пределах от 1×10-3 до 5×10-3 .
Характеристики гидромуфты Тн = f(i) и h = f(i) при wн = const имеют примерный вид, изображенный на рис. 14.4. При i > 0,95 КПД резко уменьшается и при i = 1 становится равным нулю. Это объясняется тем, что в диапазоне малых нагрузок полезная мощность на турбинном колесе стремятся к нулю, а мощность на насосном колесе уменьшается до некоторой малой, но конечной величины, расходуемой на преодоление сил трения в подшипниках и других местах муфты.
Поскольку вращающий момент Тн (см. формулу 14.3)) зависит от квадрата скорости wн, а коэффициент λ зависит от передаточного отношения i, то заводы-изготовители приводят более информативную и универсальную характеристику муфты в виде зависимостей между её безразмерными параметрами: l = f(i) и η = f(i) (рис. 14.5). Это позволяет рассчитать значения Тн при любых сочетаниях значений i и wн. Очень важно при этом знать важное свойство подобных гидромуфт - их характеристики l = f(i) и h = f(i) одинаковы. Понятие о подобии муфт будет рассмотрено ниже.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.