Из равенства (13.2):
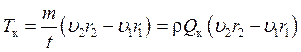, (13.3)
где m/t = rQк — массовый расход жидкости через колесо; r — плотность жидкости.
После подстановки (13.3) в (13.1) получено:
. Отсюда теоретическое давление:
. (13.4)
Выполним очевидные замены (см. рис. 13.2): r2 = R2cosa2;r1 = R1cosa1;wR2 = u2; wR1 = u1; u2cosa2 = uu2;u1cosa1 = uu1. Здесь uu1 и uu2 —проекции абсолютных скоростей на окружные. После этих замен уравнение (13.4) принимает вид:
. (13.5)
Уравнение (13.5)называют основным уравнением лопастного насоса.Оно получено Л. Эйлером в 1755 г. и связывает теоретическое давление с плотностью жидкости и её скоростью на выходе и входе колеса.
У многих насосов жидкость входит в пространство между лопатками при a1 = 90°. Тогда r1 = 0, uu1 = 0, а уравнение (13.5) упрощается до вида:
. (13.6)
При полностью перекрытом напорном трубопроводе жидкость не может выйти из колеса, вращается вместе с ним, производительность насоса Qн = 0. При этом w2 = 0; a2 = 0; u2 = u2; uu2 = u2, а теоретическое давление в напорном патрубке достигает максимума:
. (13.7)
Из основного уравнения (13.5) аналитически можно вывести зависимость расхода Qк от теоретического давления рт, размеров колеса и скорости его вращения. На практике используют характеристики насосов Qн = f(pн), полученные экспериментально.
|
Рис. 13.4. Сравнение теоретических и экспериментально полученных характеристик |
На рис. 13.4, а изображены рассчитанные (пунктирные линии) и экспериментальные (сплошные линии) характеристики тихоходного лопастного насоса. Теоретическая зависимость pт = f(Qк) существенно отличается от зависимости pн = f(Qн), полученной экспериментально. Однако в некотором диапазоне расходов Qн, соответствующем работе насоса с наибольшим КПД (номинальный режим), эти зависимости весьма близки. |
|
Рис. 13.5. Характеристики насоса рн = f(Qн) при различных частотах вращения колеса |
Заводы-изготовители приводят графики изменения давления, мощности и КПД насосов в функции их производительности при нескольких частотах вращения вала. На графиках зависимостей pн = f(Qн), построенных при различных частотах (рис.13.5), можно найти точки так называемых сходственных режимов работы, т.е. такие сочетания pн и Qн, при которых насос работает с одинаковыми значениями КПД. Например, сходственные точки А1, А2, А3 соответствуют работе насоса с частотами: n1, n2, n3(n1>n2 >n3) при одинаковых и наибольших значениях КПД. В сходственных точках, лежащих левее точек Ai, например, В1, В2, В3, и правее точек Ai (С1, С2, С3), насос работает при меньших значениях КПД. |
Точки сходственных режимов (А1, А2, А3 …, В1, В2, В3 … и т.д.) лежат на параболах, проведенных через начало координат.
35.Критерии подобия гидромеханических насосов. Соотношение между расходами, давлениями, мощностями, вращающими моментами на валу и КПД подобных насосов.
Когда говорят о подобии насосов, подразумевают подобие их проточных полостей. Как будет показано ниже, если два насоса подобны друг другу, то характеристики одного из них (производительность, давление, мощность привода) могут быть вычислены через характеристики другого. Знание соотношений между характеристиками подобных насосов существенно упрощает проектирование новых и пересчет характеристик существующих насосов при изменении частоты вращения вала.
1.Геометрическое подобие проточных полостей:
- один и тот же коэффициент пропорциональности между одноимёнными линейными размерами, зазорами и шероховатостями. Если наружный диаметр колеса натуры больше диаметра колеса модели в 2 раза, то и все остальные линейные размеры, определяющие проточную полость, должны быть больше во столько же раз. Соблюсти пропорциональность шероховатостей и зазоров, как правило, не удаётся, поэтому геометрическое подобие выполняется только для макроразмеров;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
