Размерный анализ технологических процессов механической обработки: Учебное пособие по дисциплине "Технология машиностроения", страница 4

1.3. Расчет размерных цепей методом неполной взаимозаменяемости на основе теории вероятностей

Метод расчета размерных цепей на основе теории вероятностей учитывает дей­ствительное рассеяние размеров по полю допуска и случайный характер их сочетания в размерной цепи. Следовательно, исходные условия метода в точности соответствуют тем, которые в действительности имеют место на практике, В результате этого при решении прямой задачи допуски на составляющие звенья получаются шире, а при решении обрат­ной задачи поле рассеяния замыкающего звена получается уже, чем при расчете на макси­мум-минимум. Причем этот выигрыш будет тем значительней, чем больше звеньев содер­жит размерная цепь и чем более однородны по величине допуски составляющих звеньев. Но расчет на основе теории вероятностей несколько сложнее.

В соответствии с ГОСТом 16320-80 расчетные формулы имеют следующий вид:

— номинальный размер замыкающего звена

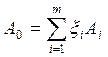
— координата середины поля допуска замыкающего звена

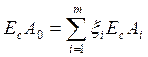
— координата центра группирования замыкающего звена

;

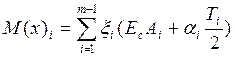— коэффициент относительной асимметрии 1-го звена

;

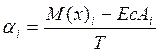берется со знаком «-» для охватывающих звеньев (отверстие α=-0,2 )

и со знаком «+» для охватываемых звеньев ( для вала α=+0,2 )

— коэффициент относительного рассеяния i-гo звена

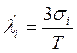
— допуск замыкающего звена

;

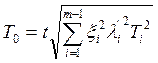— верхнее и нижнее предельные отклонения замыкающего звена

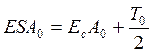
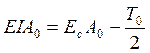
Здесь т — число звеньев размерной цепи, включая замыкающее звено. Значения остальных членов формул приведены в начале пособия.

Значения коэффициентов ξ , t, λ  и α

Передаточное отношение ξ, определяет степень влияния погрешности составляю­щего звена на погрешность замыкающего и вычисляется из следующего соотношения:

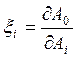; для увеличивающихся звеньев имеет знак “+”, а для уменьшающих – знак “-”

где     — погрешность замыкающего звена;

           — погрешность составляющего звена,    вызывающая погрешность .

Для линейных размерных цепей с параллельными звеньями, каковыми обычно являются тех­нологические размеры цепи, погрешность составляющего звена целиком переносится на замыкающее, т. е.  =  и, следовательно, для таких размерных цепей ξ_i =1 .

Коэффициент t учитывает риск выхода размера за установленные пределы (до­пуск). Обычно в расчетах принимают t=3. Тогда в пределах допуска по данному размеру, вероятно, окажется 99,73% всех деталей партии и, следовательно, за его пределы выйдет 0,27% или, примерно, три детали из тысячи.

Если в процессе расчета операционной размерной цепи величина рассеяния за­мыкающего звена ω₀ окажется больше допуска Т₀, заданного чертежом или технически­ми требованиями, то, подсчитав отношение Т₀/ω₀, по табл. 1 приложений можно опреде­лить количество деталей (в %), размер замыкающего звена которых окажется за предела­ми допуска.

Коэффициент относительного рассеяния i-го звена  характеризует закон рассея­ния размеров. Для некоторых теоретических распределений этот коэффициент имеет сле­дующие значения:

— для    нормального   распределения    (кривая   Гаусса) .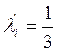

Нормальный закон распределения размеров следует использовать при крупносерийном и массовом  производстве для любого типа звеньев; и для любого типа производства – при числе звеньев более 5;

— для распределения по закону   равнобедренного   треугольника  .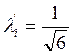

Закон равнобедренного треугольника (закон «Симпсона») следует использовать, если при изготовлении на технологический процесс постоянно оказывает влияние один или два фактора, например, износ станка;

— для распределения   по   закону    равной    вероятности.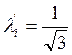

Распределение по закону равной вероятности характерно при единичном и мелкосерийном производстве.

Поскольку в расчетах размерных цепей обычно принимают t=3 (риск выхода размера за пределы установленного допуска 0,27 %), то два коэффициента t и  для удоб­ства вычислений можно заменить одним K_i, который связан с коэффициентами t и  следующей зависимостью: