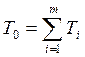Размерный анализ технологических процессов механической обработки: Учебное пособие по дисциплине "Технология машиностроения", страница 3

                                                                                                               (2)

предельные отклонения замыкающего звена:

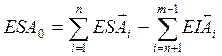                                                                                    (3)

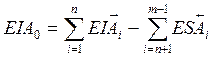                                                                                     (4)

Верхнее предельное отклонение замыкающего звена равно разности сумм верх­них отклонений увеличивающих и нижних отклонений уменьшающих звеньев; нижнее отклонение замыкающего звена равно разности сумм нижних отклонений увеличиваю­щих и верхних отклонений уменьшающих звеньев. При расчете линейных операционных размеров по ходу технологического процесса более удобны в пользовании формулы пре­дельных размеров:

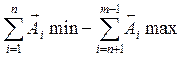                                     min (или  min) =                 (5)

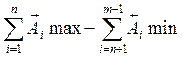                                  max (или  max) =                   (6)

Наименьший размер замыкающего звена равен разности сумм наименьших увеличивающих и  наибольших уменьшающих значений составляющих звеньев; наибольший — разности сумм наибольших увеличивающих  и наименьших уменьшающих звеньев.

Как указывалось, в технологических размерных цепях замыкающими звеньями мо­гут быть конструкторский размер А₀ или припуск на обработку Z₀, что, и отражено в фор­мулах (1), (5) и (6).

Пользуясь приведенными формулами, можно решать два типа задач — прямую и обратную, которые формулируются следующим образом.

Прямая задача: известно исходное звено; требуется определить номинал и пре­дельные отклонения неизвестного составляющего звена (неизвестных звеньев может быть несколько). Такие задачи приходится решать при проектировании механизма или техно­логического процесса.

Обратная задача: известны номинальные размеры и предельные отклонения со­ставляющих звеньев; требуется определить номинал и предельные отклонения замыкаю­щего звена. Такие задачи решаются при проверочных расчетах.

Использование приведенных формул покажем на следующем примере.

Обрабатывается партия валиков. В соответствии с чертежом (рис. 1,а) выполняются размеры:

А₁=100_-0.87 мм,     А₂=32^+0.39 мм, и А₃=40_-0.39 мм.

Требуется определить, каким может получиться размер А₀ у различных валиков.       Задача обратного типа. Замыкающим звеном является А₀, составляющими зве­ньями будут: А₁ — увеличивающее; А₂ и А₃ — уменьшающие.

                    В соответствии с формулой (1) номинал замыкающего звена равен:

А₀=А₁-(А₂+А₃)=100-(32+40)=28 мм

В соответствии с формулой (2) допуск замыкающего звена равен:

Т=Т₁+Т₂+Т₃ = 0,87 + 0,39 + 0,39=1,65 мм.

Согласно формулам (3 и 4), предельные отклонения замыкающего звена равны:

ESA₀ = ESA₁ - (ЕIА₂ + ЕIА₃)= 0 - [0 + (- 0,39)] = 0,39 мм;

EIA₀= EIA₁-(ESA₂ + ESA₃)= -0,87 - (0,39 + 0) = -1,26 мм.

Следовательно, А₀= мм.

Проверка. Задача решена правильно, если разность верхнего и нижнего отклоне­ний будет равна ранее определенной величине допуска замыкающего звена. В нашем случае 0,39-(-1,26)=1,65=Т, следовательно, решение правильное.

Заметим, что результат будет тот же, если для решения задачи воспользоваться формулами (5) и (6).

Для решения прямой задачи используются те же формулы.

Расчет размерных цепей на максимум и минимум, будучи весьма простым, имеет существенный недостаток. Если производить расчет исходя из допуска исходного звена, то допуски на составляющие звенья получаются неоправданно жесткими; если опреде­лять поле рассеяния замыкающего звена исходя из допусков составляющих звеньев, то оно получится слишком широким.

Такое несоответствие расчетных и фактических результатов объясняется малой вероятностью исходных положений, принятых в основу метода, а именно:

а) расчет размерных цепей ведется по предельным отклонениям размеров — зве­ньев (без учета фактического рассеяния размеров по полю допуска);

б)  считается, что операционные размеры сочетаются самым неблагоприятным образом, т. е., если в одной ветви размерной цепи встретились все размеры, имеющие наибольшие предельные значения, то в другой ветви окажутся все размеры, имеющие наименьшие предельные значения. Такое сочетание размеров маловероятно.