ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ ЕСТЕСТВЕННЫХ НАУК

ЯМР  СПЕКТРОСКОПИЯ

методическое пособие

к практикумам

“Химическая термодинамика” и “Химическая кинетика”

Новосибирск

2009

Составители

Доктор химических наук,  А.Г. Степанов

Доктор химических наук,  Е.П. Талзи

Ответственный за выпуск Н.В.  Ложкина

                          ©  Новосибирский государственный университет, 2009

ВВЕДЕНИЕ

Явление ядерного магнитного резонанса (ЯМР) может наблюдаться для любого атома, имеющего ядро с ненулевым угловым моментом, или, что эквивалентно, магнитным дипольным моментом. Примерами таких атомов могут быть элементы с нечетным атомным номером, такие как водород, углерод-13, азот-15, кислород-17 и т.д.

Для обнаружения явления ЯМР образец помещают в магнитное поле, которое ориентирует магнитные диполи ядер. При этом происходит расщепление магнитных подуровней ядра. При облучении образца электромагнитным полем происходит поглощение энергии  в соответствии с условием

                                                   (1)

где h – постоянная Планка, ν_I – частота резонанса ядра I, g_I – ядерный g‑фактор, β – ядерный магнетон Бора, Н₀ – внешнее магнитное поле.

Изменяя частоту ν_I или величину магнитного поля Н₀, мы поочередно можем подобрать условия выполнения (1) для всех типов ядер данного сорта изучаемого образца. Образуется спектр ЯМР, в котором каждому типу резонирующих ядер данного сорта соответствует пик поглощения.

В принципе, ЯМР может наблюдаться на магнитных ядрах любых элементов. Практические ограничения связаны с малой интенсивностью линий ЯМР из-за низкого естественного содержания большинства магнитных изотопов, большой шириной линии, большим временем спин-решеточной релаксации и некоторыми другими причинами.

В таблице приведены характеристики некоторых ядер ряда элементов, применяемых в технике ЯМР. Наибольшее распространение имеет магнитный резонанс на ядрах ¹Н, ¹³С, ¹⁵N, ²⁷Al, ²⁹Si, ³¹P, ⁵¹V и др.

Таким образом, ЯМР дает информацию о присутствии в веществе элементов, ядра которых обладают магнитными моментами. Поэтому этот метод, прежде всего, - метод качественного и количественного анализа различных веществ, дающий информацию об их составе, структуре молекул, содержании магнитных изотопов. Для аналитических целей наиболее пригодны жидкие образцы. Это связано с тем, что в жидкости из-за быстрого движения усредняются до нуля магнитные поля, создаваемые в месте расположения ядра соседними ядрами. Вследствие этого наблюдаемые линии ЯМР спектров является узкими. В твердых телах такого усреднения нет, и поэтому для них линии спектров ЯМР, как правило, значительно шире. Типичная ширина линии ЯМР для кристаллов составляет 20‑45 кГц; ширина линии в спектрах высокого разрешения жидкости не превышает 1 Гц.

Таблица

Изотопы	Спин ядра	Резонансная частота νI для Н0 = 9,39798 T, МГц	Естественное содержание, %	Чувствительность S отн. 1Н
1H	1/2	400,130	99,9885	1,00
2H	1	61,422	0,0115	1,45·10−6
13C	1/2	100,613	1,07	1,76·10−4
15N	1/2	40,560	0,364	3,85·10−6
19F	1/2	376,498	100	8,32·10−1
27Al	5/2	104,261	100	2,07·10−1
31P	1/2	161,976	100	6,65·10−2
195Pt	1/2	86,015	33,832	3,36·10−3

1. ЯДЕРНЫЙ МАГНИТНЫЙ МОМЕНТ

Любое движение заряженного тела создает магнитное поле. Для описания магнитного поля, создаваемого замкнутым витком проводника с током, удобно приписать этому витку соответствующий дипольный магнитный момент. Это явление имеет место и в атомном масштабе. Если электроны и ядра обладают угловым моментом, они имеют и магнитный момент. Величину этого магнитного момента легко оценить с классической точки зрения для орбитального движения электрона.

Предположим, электрон движется по круговой орбите с угловой скоростью ω. Такое движение эквивалентно электрическому току в противоположном направлении с величиной . Орбитальный угловой момент, обозначенный , есть ;  – масса электрона,  – расстояние от ядра. Таким образом, электрический ток может быть выражен следующий образом:

                                          (1.1)

Из электродинамики известно, что замкнутый виток с током  обладает магнитным моментом 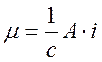, где А – площадь, охватываемая витком, с – скорость света. В нашем случае , тогда

,                                               (1.2)

 и  – антипараллельные векторы для электронов. В атомной шкале угловой момент квантуется в величинах . Следовательно, магнитный момент квантуется в величинах (магнетон Бора).