ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”, страница 8

В идеально однородном поле постоянная времени спада была бы равна , однако фактически сигнал свободной индукции спадает с характеристическим временем , которое часто определяется, прежде всего, неоднородностью магнитного поля. Вследствие неоднородности, магнитное поле в различных точках ампулы ЯМР разное. 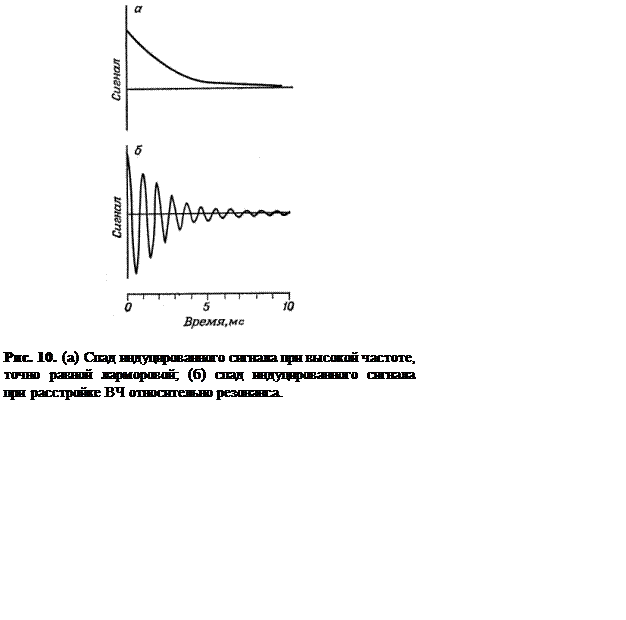Ядра в разных полях прецессируют с разными частотами, при этом веер магнитных моментов  () быстро расходится и М стремится к нулю. На Рисунке 10а показан чисто экспоненциальный спад сигнала, который получается, если частота ВЧ-импульса в точности равна резонансной частоте единственного типа ядер в образце. Хотя регистрация сигнала производится в отсутствии непосредственного воздействия ВЧ, опорный ВЧ-сигнал подается на детектор непрерывно, и поэтому детектор реагирует только на ту компоненту намагниченности, которая лежит вдоль оси у' во

вращающейся системе координат. Если частота ВЧ-импульса слегка отличается от частоты опорного сигнала, то сразу после 90°-го импульса  будет лежать вдоль оси у'. Однако  теперь вращается относительно вращающейся системы координат c частотой, равной разнице частот ВЧ‑импульса и опорного сигнала, и детектор выделяет не только экспоненциальный спад М_ху, но и эффект интерференции с опорным сигналом (Рисунок 10б). Спад М, следующий за 90°-м импульсом, несет спектральную информацию, выявляемую в Фурье-спектроскопии ЯМР.

Строго доказано, что преобразование Фурье спада свободной индукции дает спектр ЯМР, полностью эквивалентный тому, который получается при медленном прохождении резонанса на спектрометрах с непрерывной разверткой. В ЯМР спектрометрах с непрерывной развёрткой частота приложенного электромагнитного поля с магнитной составляющей Н₁ медленно меняется и последовательно выписываются пики поглощения энергии приложенного поля при достижении условий резонанса для различных типов протонов. В импульсных ЯМР спектрометрах образец поглощает энергию ВЧ‑импульса, который формируется при быстром включении и выключении передатчика, работающего на частоте, близкой к резонансной для данных ядер. После прекращения импульса, энергия, полученная образцом, возвращается в катушку приёмника в виде электрического сигнала, который называется спадом свободной индукции.

Как правило, импульсная ЯМР спектроскопия трудно воспринимается студентами. Поэтому в следующем разделе мы более подробно остановимся на том, как формируется спад свободной индукции, и как из него получают спектр ЯМР.

3.5. Действие радиочастотных импульсов и преобразование Фурье

Разложение в ряд Фурье – это математический метод разложения сложного колебания на его спектральные компоненты. Функцию  обычно можно представить в виде ряда Фурье, т.е. бесконечного ряда синусов и косинусов:

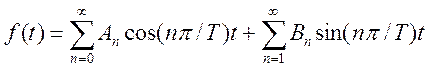                    (3.13)

Когда проводятся математические операции спектрального анализа, то удобнее иметь дело не с рядами Фурье, а с соответствующими интегралами, в которых снято ограничение на область определения входящих в них функций: переменная t не ограничена областью , а может изменяться в бесконечных пределах. В этом случае

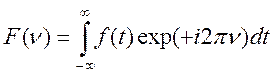
и                                                                                                     (3.14)

.

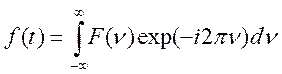Осуществляя преобразования Фурье сложного колебания , получают частотный спектр этого колебания , т.е. в случае спада сигнала свободной индукции – спектр ЯМР. Действительно, преобразование Фурье представляет спад свободной индукции как сумму синусоид с различными весами и частотами, т.е. в виде спектра ЯМР. Каждому пику соответствует синусоида определённой частоты, интенсивность пика соответствует весу этой синусоиды, а ширина пика определяется скоростью затухания синусоиды.