G = u + iv:
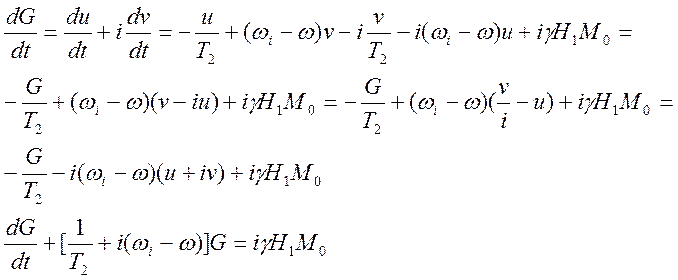 (4.1)
(4.1)
Обозначим ![]()
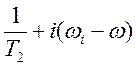 (4.2)
(4.2)
Если перехода между двумя состояниями А и В не происходит, то имеются две независимых макроскопических намагниченности, которым отвечают две комплексные величины GA и GB
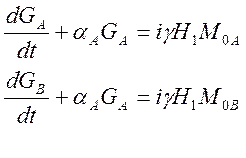 (4.3)
(4.3)
![]()
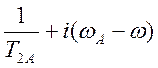 (4.4)
(4.4)
![]()
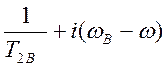 (4.5)
(4.5)
T2A и Т2B – времена релаксации состояний А и В в отсутствие обмена. В результате обмена ядра переходят из положения А в В и наоборот. Разумно предположить, что в процессе обмена перескок происходит мгновенно и для него необходимо время гораздо меньшее, чем период ларморовской прецессии. Пусть tА – среднее время жизни ядра в состоянии А, tВ – среднее время жизни ядра в состоянии В, 1/tА – вероятность перехода ядра из состояния А в состояние В в единицу времени, 1/tВ – то же для перехода из В в А
|
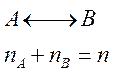 (4.6)
(4.6)
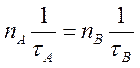 ;
; 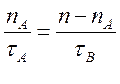 (4.7)
(4.7)
 – вероятность нахождения ядра в состоянии А; (4.8)
– вероятность нахождения ядра в состоянии А; (4.8)
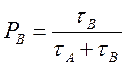 – вероятность нахождения ядра в состоянии B; (4.9)
– вероятность нахождения ядра в состоянии B; (4.9)
Если учесть обмен между двумя состояниями, то уравнения Блоха для GA и GB видоизменятся следующим образом:
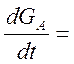
![]() -
-![]()
![]()
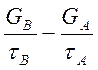 (4.10)
(4.10)
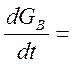
![]() -
-![]()
![]()
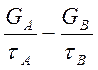 (4.11)
(4.11)
Найдем решение этих уравнений для случая медленного прохождения резонанса. Ситуация обычно реализуемая в ЯМР-спектроскопии. При реализации условий медленного прохождения
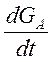 =
=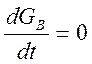 (4.12)
(4.12)
![]()
![]() −
−![]()
![]()
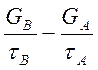 (4.13)
(4.13)
![]()
![]() −
−![]()
![]()
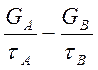 (4.14)
(4.14)
Учитываем, что ![]() ,
, ![]() , и
суммируем уравнения (4.13) и (4.14)
, и
суммируем уравнения (4.13) и (4.14)
![]() ; (4.15)
; (4.15)
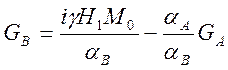 (4.16)
(4.16)
Значение ![]() подставляем в уравнение (4.13)
подставляем в уравнение (4.13)
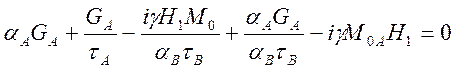 , (4.17)
, (4.17)
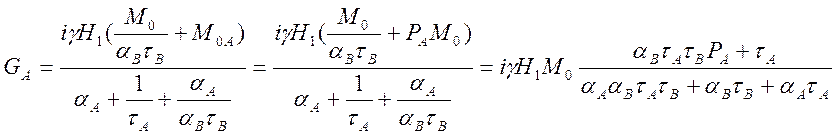 В знаменателе данного выражения добавим и
вычтем 1 и получим:
В знаменателе данного выражения добавим и
вычтем 1 и получим:
![]()
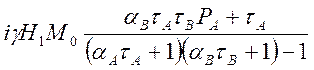 (4.18)
(4.18)
Зная ![]() , находим
, находим ![]() .
.
![]() =
=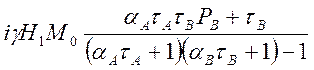 (4.19)
(4.19)
Полный комплексный момент единицы объема образца при наличии обмена
![]()
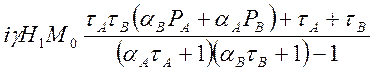 (4.20)
(4.20)
![]() (4.21)
(4.21)
Медленный обмен
![]() и
и ![]() >>
>> ![]() (4.22)
(4.22)
Такой случай
возможен, когда ![]() является большой величиной. В
этом случае, если
является большой величиной. В
этом случае, если ![]() близка к
близка к ![]() ,
то
,
то ![]() очень сильно отличается от
очень сильно отличается от ![]() . Следовательно, состояние ядер В
далеко от резонансного. В этом случае проекция намагниченности
. Следовательно, состояние ядер В
далеко от резонансного. В этом случае проекция намагниченности ![]() на оси х и у близка к нулю.
Поэтому в момент прохождения сигнала А
на оси х и у близка к нулю.
Поэтому в момент прохождения сигнала А ![]() , и
наоборот. Таким образом, в спектре, как и в отсутствие обмена, наблюдаются два
сигнала – А и В. Однако обмен отразится на форме сигнала. При
медленном прохождении
, и
наоборот. Таким образом, в спектре, как и в отсутствие обмена, наблюдаются два
сигнала – А и В. Однако обмен отразится на форме сигнала. При
медленном прохождении 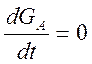 и
и
из формулы (4.13) следует, что
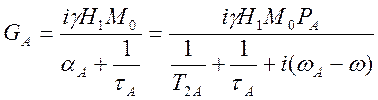 (4.23)
(4.23)
Обозначим 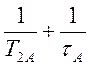 как
как ![]() . Тогда
. Тогда
 (4.24)
(4.24)
Чтобы
определить, какова будет форма линии, определим проекцию намагниченности ![]() на ось у, которая является мнимой
частью
на ось у, которая является мнимой
частью ![]()
![]() . Для этого можно
воспользоваться соотношением
. Для этого можно
воспользоваться соотношением
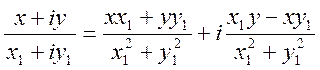 (4.25)
(4.25)
Используя (4.25), находим
![]()
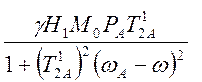 (4.26)
(4.26)
Видно, что форма
линии Лоренцева, но с шириной ![]() =
=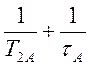
![]()
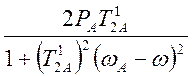 (4.27)
(4.27)
Таким образом,
резонансная полоса (max. ![]() лежит
при
лежит
при ![]() Найдем ширину резонансного сигнала на
полувысоте. Высота при
Найдем ширину резонансного сигнала на
полувысоте. Высота при ![]() есть
есть ![]()
![]() . Половину высоты резонансный сигнал будет
иметь при
. Половину высоты резонансный сигнал будет
иметь при ![]() , определяемом из соотношения
, определяемом из соотношения
![]()
![]()
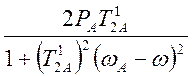 (4.28)
(4.28)
Из этого соотношения следует, что
![]()
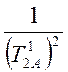 ; (4.29)
; (4.29)
![]()
![]()
![]() ; (4.30)
; (4.30)
![]()
![]() ;
; ![]()
![]() ; (4.31)
; (4.31)
![]()
![]() или
или ![]()
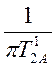 . (4.32)
. (4.32)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.