Другие предметы \ Спектроскопия ядерного магнитного резонанса

ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”, страница 21

При этом для скорости спин-спиновой релаксации (1/Т2) сигнала ЯМР ОН-группы енола или сигнала СН2‑группы кетона справедливо соотношение

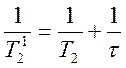                                                      (9.18)

Здесь  – скорость релаксации при отсутствии обмена,  – наблюдаемая скорость релаксации при наличии обмена; t – время жизни протона в кето- или енольной форме ацетилацетона, величина  равна константе скорости реакции k1 или k2. Так как величина Т2 связана с шириной линии ЯМР соотношением

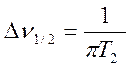,                                                     (9.19)

то выражение (9.6) можно представить в виде

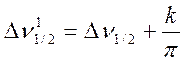                                             (9.20)

Здесь  – ширина линии OH-группы енола или СН2-группы кетона при отсутствии обмена;  – та же величина, но при наличии обмена между кето- и енольными формами ацетилацетона.

В первом приближении можно считать, что  равна ширине ОН- или СН2-линий ацетилацетона при отсутствии добавок диэтиламина. Вычитая ширину линий ОН или СН2 ацетилацетона без добавок диэтиламина из ширины этих линий, но в присутствии добавок диэтиламина, можно определить константы скорости обмена кето- и енольной форм ацетилацетона, а анализируя температурную зависимость , легко получить значение энергии активации реакций превращения кето-формы ацетилацетона в енольную форму и наоборот.

Методика проведения эксперимента

1. Приготовить два образца в 5 мм ампулах ЯМР:

А:  0,5 мл ацетилацетона + 0,025 мл ГМДС или ТМС;

Б:  0,3 мл ацетилацетона + 0,2 мл диэтиламина + 0,025 мл ГМДС.

2. Записать спектры ЯМР двух образцов и сделать отнесение сигналов к кето- и енольной формам при T = 294 К.

3. Измерить ширины линий ОН- и СН2-групп ацетилацетона без добавок диэтиламина (образец "А") и считать, что она не меняется при изменении температуры.

4. Измерить ширины линий ОН- и СН2-групп ацетилацетона в присутствии диэтиламина (образец "Б").

5. Определить k1 и k2 по формуле (9.20).

6. Увеличить температуру на 5‑6 градусов и вновь измерить ширины линий, определить k1 и k2.

7. Получить 7‑10 значений  для кето- и енольной форм до температуры »340 К и в каждом случае определить k1 и k2.

8. Результаты оформляют в виде таблицы:

T, K

k1

k2

9. Строят линейную анаморфозу (lnk; 1/Т) и обрабатывают ее по методу наименьших квадратов (выражения (9.4)-(9.6)). Получают значения энергии активации Е1 и Е2 и величины предэкспоненциальных множителей  и , а также значения ошибок для Е1, Е2,  и . Результаты заносят в таблицу:

Е1

Е2

ЛАБОРАТОРНАЯ РАБОТА Я-5

Определение скорости и энергии активации диссоциации бипиридината бис(ацетилацетоната) никеля(II) Ni(асас)2Ру2

Процесс координации пиридина (Ру) к комплексу Ni(acac)2Py2 описывается уравнением

 


M + L   ↔    ML,

где М = Ni(асас)2Ру2, L = Ру, К – константа устойчивости, определяемая как:

K = 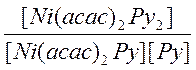 >> 102

Обмен Ру между раствором и координационной сферой Ni(II) является быстрым в шкале времени ЯМР. В соответствии с этим парамагнитный сдвиг ядер Ру определяется выражением

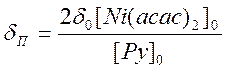,                                         (9.21)

а ширина линии по уравнению (7.4), где состояния А и В относятся к координированному и свободному состояниям Ру соответственно.

Для выполнения измерений времен обмена и энергий активации необходимо измерить парамагнитный сдвиг и ширину линии a‑протона Ру в диапазоне температур от 30 до 70 °С. Из этих данных можно найти kдис. и Eдис., если в свободном состоянии хим. сдвиг Ру составляет 516 Гц, а ширина линии a‑протона равна 2 Гц.

Методика выполнения эксперимента

Скачать файл