ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”, страница 6

3. ВВЕДЕНИЕ В ИМПУЛЬСНУЮ ЯМР СПЕКТРОСКОПИЮ

3.1. Уравнение Блоха

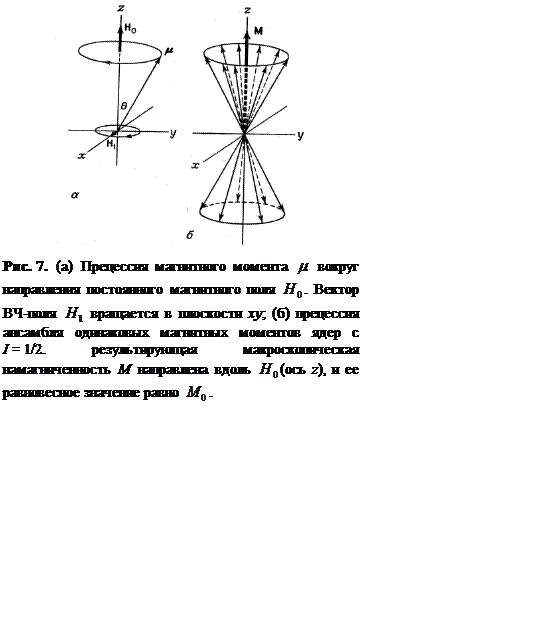
Классическое рассмотрение движения магнитного момента в магнитном поле Н₀ необходимо для понимания импульсной ЯМР фурье спектроскопии, поэтому остановимся на этом рассмотрении более подробно.

Рассмотрим поведение макроскопического образца, содержащего много идентичных молекул, каждая из которых имеет одно магнитное ядро. Общий магнитный момент или намагниченность  образца – это результирующая ядерных моментов :  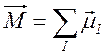       (Рисунок 7) или в терминах полного спинового углового момента

.                                                   (3.1)

Поскольку образец макроскопический, действие на  него внешнего магнитного поля  может быть описано законами классической механики. Изменение углового момента  во времени зависит от крутящего момента , действующего на магнитный момент со стороны приложенного поля

,

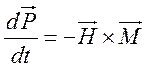используя

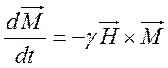.                                             (3.2)

Квазистационарное решение уравнения (3.2) представляет собой прецессию  вокруг направления магнитного поля с угловой частотой . Частота  называется ларморовской частотой.

Уравнения движения магнитного момента  должны включать приближение его к термодинамически равновесному значению . Если поле  направлено вдоль оси , то очевидно, что , где 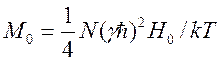, N – полное число спинов,  и . Блох предположил, что проекции  стремятся к равновесным значениям экспоненциально. Причем  и ,  изменяются с разными характерными временами  и , соответственно.

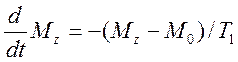                                            (3.3)

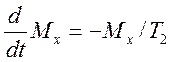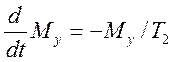;                         (3.4)

Приближение к термодинамическому равновесию называют релаксацией и времена  и  – временами релаксации. Скорость релаксации продольной компоненты  может отличаться от скорости релаксации поперечных компонент ( и ).

Энергия спиновой системы в поле , направленном вдоль оси z, зависит только от . Любые изменения М_z сопровождаются потоком энергии от системы ядерных спинов к другим степеням свободы, по историческим причинам называемым "решеткой". Время релаксации  обычно называют временем спин-решеточной релаксации или временем, продольной релаксации.  известно как время поперечной или спин-спиновой релаксации. Последнее название возникло потому, что для протонов в твердом теле прямые взаимодействия между спинами различных ядер вызывают релаксацию  и  без переноса энергии к решетке,  < . В невязких жидкостях обмен энергии с решеткой влияет как на , так и на , причем  » T₂.

В экспериментах по ядерному магнитному резонансу слабое осциллирующее магнитное поле  прикладывается в направлении оси х (Рисунок 7). Это поле можно разложить на две компоненты, вращающиеся в противоположных направлениях с угловыми частотами . Компонентой, вращающейся в направлении, противоположном ларморовской прецессии, можно пренебречь. Вращающееся магнитное поле индуцирует вращающуюся намагниченность в плоскости ху, которая фиксируется спектрометром. Следует подчеркнуть, что как стационарный, так и импульсный ЯМР спектрометры устроены так, что измеряют изменение намагниченности именно в плоскости ху.

Магнитное поле, действующее на  образец,  может быть представлено как

                                (3.5)

где , ,  – единичные векторы в направлении х, у, z.

Комбинируя уравнения (3.2), (3.3), (3.4) и вспоминая правила определения компонент векторного произведения , получаем уравнения Блоха:

;

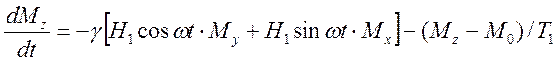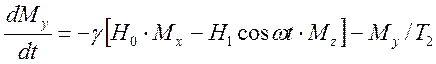                                (3.6)

.

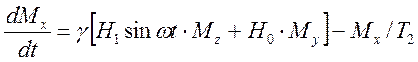3.2. Вращающаяся система координат

Уравнения Блоха имеют более простую форму, если они записываются в системе координат , , , вращающейся с угловой скоростью  вокруг оси . Эта скорость вращения по величине и направлению совпадает со скоростью вращения поля . Именно такая система координат используется при детектировании сигнала ЯМР, когда из сигнала вычитается опорная частота .