ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”, страница 20

Со(асас)₂Ру₂ + СН₂С1₂   ↔   [Co(acac)₂Py₂]·CH₂Cl₂                 (9.15)

Парамагнетизм Со(асас)₂Ру₂ приводит к тому, что линия СН₂Сl₂ в комплексе с Со(асас)₂Ру₂ должна быть сдвинута на 28 м.д. в слабое поле по сравнению с сигналом свободного СН₂Сl₂. Однако, поскольку имеет место быстрый в шкале времени ЯМР обмен молекулы СН₂Сl₂ между координированным и свободным состояниями, в спектре ЯМР наблюдается одна линия, положение которой будет зависеть от соотношения концентраций в растворе СН₂Сl₂ и [Со(асас)₂Ру₂]·СН₂Сl₂.

При выполнении условия [Со(асас)₂Ру₂] << [СН₂Сl₂] для величины наблюдаемого парамагнитного сдвига СН₂Сl₂ справедливо следующее выражение:

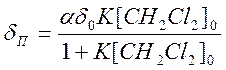                                          (9.16)

где  – разность сдвигов линии ЯМР СН₂Сl₂ в присутствии Со(асас)₂Py₂ в растворе и в его отсутствие (диамагнитный растовор); a = [Со(аcас)₂Ру₂]₀/[CH₂Cl₂]₀; d₀ – величина парамагнитного сдвига СН₂Сl₂ в комплексе с Со(асас)₂Ру₂, d₀ = 28 м.д.

Величина константы равновесия К для реакции (9.15) К » 3 М⁻¹. Тогда при концентрации [СН₂Сl₂] » 0,1 М будет справедливо соотношение K·[CH₂Cl₂] << 1, и выражение (9.16) можно переписать как

                                           (9.17)

Из выражения (9.17), зная величины a, d₀, [СН₂Сl₂]₀, по экспериментально определяемому параметру  легко получить точное значение К. Величина K связана с изменением термодинамических потенциалов соотношением (9.3).

Таким образом, определяя из эксперимента величину парамагнитного сдвига  при фиксированной температуре, можно получить температурную зависимость константы равновесия К для реакции (9.15), а затем вычислить параметры  и .

Методика проведения эксперимента

1. Готовят два раствора в С₆H₁₂ объемом 0,6 мл:

образец А:  [Со(асас)₂]₀ = 2×10⁻³M; [Py]₀ = 0,05 M; [СН₂Сl₂]₀ = 0,1 М;

образец Б:  [СН₂Сl₂]₀ = 0,1 М; [Py]₀ = 0,05 M.

Добавляют в оба раствора по ~0,05 мл внутреннего эталона ГМДС или ТМС.

2. Записывают спектр ЯМР образца А при фиксированной температуре (T = 25 °С), измеряют расстояние в герцах между линиями СН₂Сl₂ и С₆Н₁₂.

3. Записывают спектр образца Б и вновь измеряют расстояние между линиями СН₂Сl₂ и С₆Н₁₂. Разность расстояний между линиями образца А и Б представляет собой парамагнитный сдвиг.

4. Повышают температуру на 6‑8 °С и вновь записывают спектр ЯМР двух образцов и вычисляют величину .

5. Получают зависимость К = f(Т) в 5‑10 точках до температуры 75 °С.

6. Вычисляют величины К по формуле (9.16) при каждой температуре.

7. Строят линейную зависимость RlnK от 1/Т по методу наименьших квадратов (9.4). Из отсекаемого отрезка и тангенса угла наклона зависимости R1nК от 1/Т получают величины  и  и определяют величины стандартных отклонений и  по формулам (9.4)-(9.6).

В этих формулах y = RlnK; x = 1/T; p = ; q = ;n – число точек в эксперименте.

8. Результаты заносят в таблицу

T, K	K, M−1

ЛАБОРАТОРНАЯ РАБОТА Я-4

Определение кинетических параметров процесса кето-енольной таутомерии ацетилацетона в присутствии диэтиламина

Процесс кето-енольной таутомерии ацетилацетона можно рассматривать как перенос протона согласно реакции (9.1). В отсутствие каких-либо добавок время жизни каждого из состояний весьма велико (несколько секунд, k₁ и k₂ – малы, и в спектре ЯМР ¹Н наблюдаются две группы линий, относящиеся к протонам кето- и енольных форм. Добавление диэтиламина в ацетилацетон приводит к ускорению прямой и обратной реакции (9.1). При этом в спектре ЯМР наблюдается слияние сигналов СН₃‑групп и уширение ОН‑сигнала енола и СН₂‑сигнала кето-формы, а также их сдвиг навстречу друг другу.