Таким образом, в
отсутствие обмена ширину линии ЯМР характеризует величина ![]() , при наличии обмена – величина
, при наличии обмена – величина ![]() =
=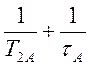 . При наличии медленного
обмена наблюдаем два сигнала вблизи
. При наличии медленного
обмена наблюдаем два сигнала вблизи ![]() и
и ![]() , но уширенные. По уширению сигнала можно
определить времена жизни состояний. Для сигнала А
, но уширенные. По уширению сигнала можно
определить времена жизни состояний. Для сигнала А
![]() −
− ![]() =
= 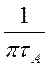 (4.33)
(4.33)
Аналогично для сигнала В.
Быстрый обмен
Это случай,
когда ![]() и
и ![]() <<
<< ![]() . (4.34)
. (4.34)
Eсли ![]() и
и ![]() ®
0, в выражении для G можно
приравнять нулю все члены, содержащие произведение
®
0, в выражении для G можно
приравнять нулю все члены, содержащие произведение ![]() .
.
G = 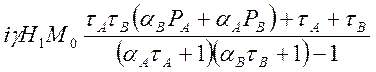 =
= 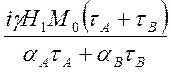 =
=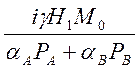 .
.
Подставим ![]()
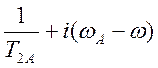 ;
; ![]()
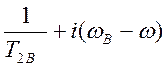 и получим
и получим
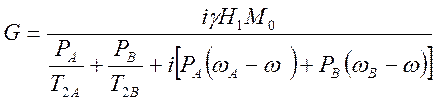 (4.35)
(4.35)
Обозначим 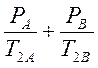 =
=![]() и учтём, что PA + PB = 1,
тогда
и учтём, что PA + PB = 1,
тогда
![]()
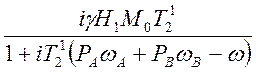 (4.36)
(4.36)
Ищем мнимую часть G
V = 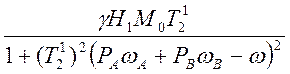 (4.37)
(4.37)
Анализируем форму линии
g(w) = 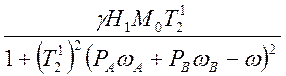 (4.38)
(4.38)
Ищем положение максимума поглощения:
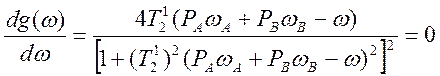 (4.39)
(4.39)
Таким образом, будет наблюдаться один максимум поглощения при ![]()
Ищем ширину
сигнала на полувысоте, учитывая что 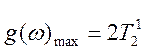 .
.
Ищем значения w, при которых 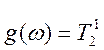
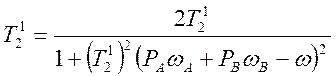 (4.40)
(4.40)
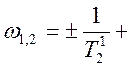
![]() ;
; 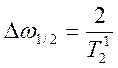 ;
; ![]() v1/2 =
v1/2 = ![]() , где
, где 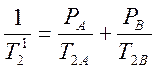 .
.
Таким образом, в случае очень быстрого обмена ширина линии не зависит от tА и tВ.
Промежуточная скорость обмена
Пусть![]() и
и ![]() имеютпорядок
имеютпорядок![]() .
.
Вернёмся к выражению
G = 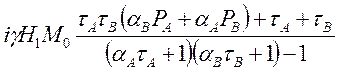
и проанализируем
частный случай 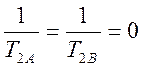 , PA
= PB =1/2,
, PA
= PB =1/2, ![]() =
= ![]() =2t.
=2t.
Тогда ![]() ;
; ![]() .
.
Преобразуем знаменатель
![]() =
= ![]() =
=
=![]()
![]() . (4.41)
. (4.41)
Преобразуем числитель
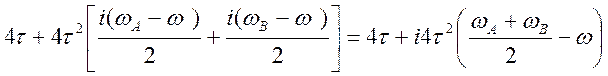 (4.42)
(4.42)
Сокращаем на 4![]() и получаем
и получаем
G = 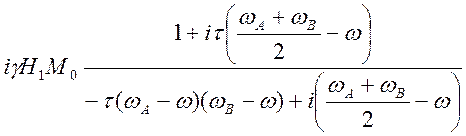 (4.43)
(4.43)
Переписываем в другом виде
G = 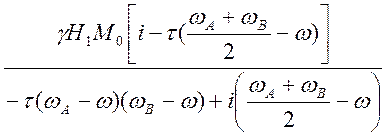 и ищем мнимую часть
и ищем мнимую часть
V = ![]()
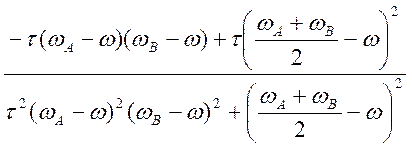 (4.44)
(4.44)
Преобразуем числитель
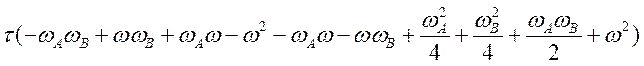 =
=
= 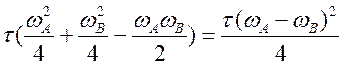
V = ![]()
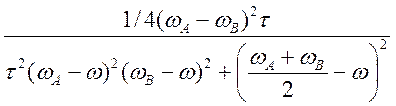 (4.45)
(4.45)
Переходим от ![]() к n
и анализируем форму линии
к n
и анализируем форму линии
g(n)
= 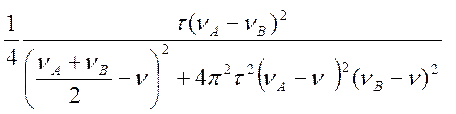 . (4.46)
. (4.46)
Ищем
экстремальные точки функции g(n) из условия 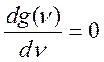 .
.
Обозначим знаменатель буквой z. Тогда
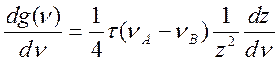 (4.47)
(4.47)
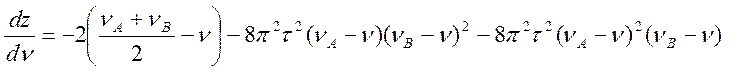 = 0
= 0
![]()
![]()
![]() -
-![]() [
[![]()
+![]()
![]() ] = 0 (4.48).
] = 0 (4.48).
![]() −
−![]() [
[![]() +
+
+![]() ] = 0 (4.49)
] = 0 (4.49)
![]()
+![]() } = 0 (4.50)
} = 0 (4.50)
Разделим обе части уравнения на 4p2t2
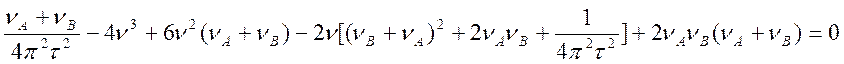
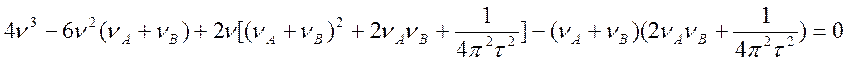
Пусть ![]() ,
, 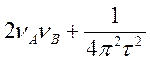 = В,
тогда
= В,
тогда
![]() (4.51)
(4.51)
![]() (4.52)
(4.52)
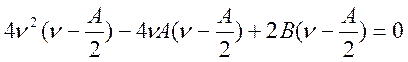 (4.53)
(4.53)
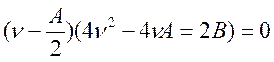 (4.54)
(4.54)
Найдём корни уравнения (4.53).
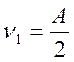 ;
; 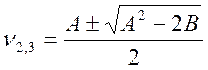 . (4.55)
. (4.55)
Все решения имеют физический смысл, если А2 ³ 2В. При А2 = 2В происходит слияние сигналов. n1 = n2 = n3.
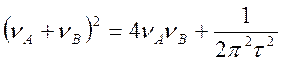 (4.56)
(4.56)
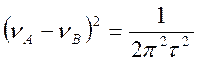 (4.57)
(4.57)
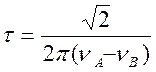 (4.58)
(4.58)
При больших t наблюдаются два сигнала, расстояние между которыми
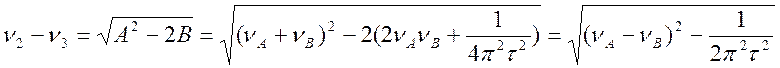
или 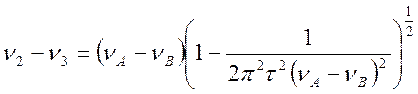 (4.59)
(4.59)
Таким образом, в случае промежуточного обмена расстояние между сигналами является функцией 2pt(nА-nВ).
Следует помнить, что в рассматриваемом частном случае величина t связана со среднем временем жизни ядра в состоянии A (tА) соотношением tА = 2t.
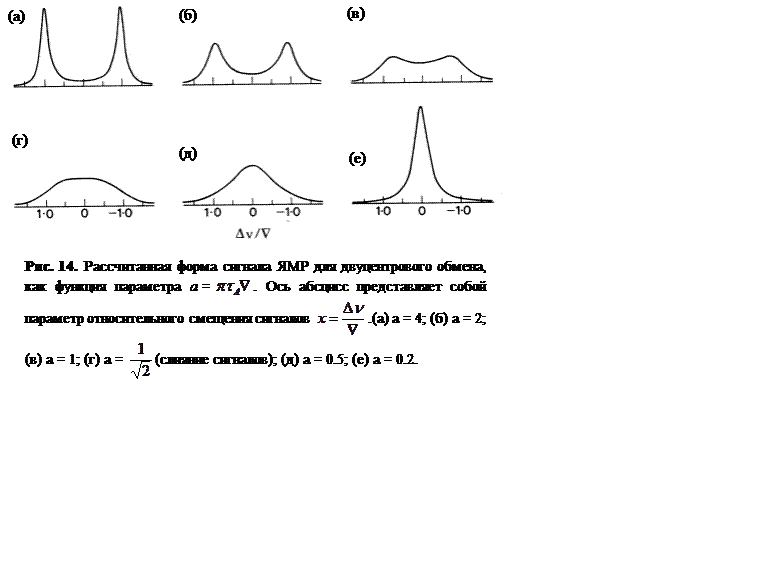
Для наглядного представления формы сигнала, возникающего при различных скоростях обмена, проанализируем более детально функцию формы линии
g(v)
= 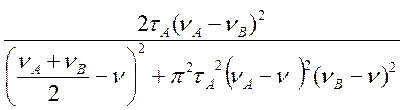 (4.60)
(4.60)
Эту функцию
можно представить как функцию безразмерного переменного 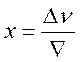 и
параметра
и
параметра ![]() , где
, где 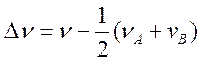 и
и 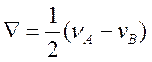 .
.
Тогда
 |
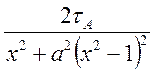 . (4.61)
. (4.61)
На Рисунке 14 представлена рассчитанная форма сигнала g(x) , как функция
параметра a = ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.