ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”, страница 2

При рассмотрении магнитного момента, связанного с собственным угловым моментом (спином) электрона, классическое рассмотрение не воспроизводит связь углового и магнитного моментов. Удобно ввести фактор  и представить связь магнитного момента со спином электрона :

,                              (1.3)

где  для свободного электрона составляет  = 2,0023.

Аналогичное выражение может быть использовано для связи спинового движения ядер с соответствующим магнитным моментом

 ~,                                                    (1.4)

 – масса ядра,  – заряд. В качестве единицы магнитного момента ядра удобно использовать магнитный момент протона (ядерный магнетон):

,                                                      (1.5)

где  – масса протона.

Для других ядер разница в массе и в заряде включается в ядерный g – фактор ():

                                                       (1.6)

Обычно для записи выражения, связывающего магнитный момент ядра с его угловым моментом, в спектроскопии ЯМР вместо  используется гиромагнитное отношение

                                                                   (1.7)

1.1. Ядра в магнитном поле

В отсутствие магнитного поля энергия ядра не зависит от квантового числа . Это эквивалентно утверждению, что энергия магнита не зависит от его ориентации в отсутствие магнитного поля.

Когда магнитное поле Н₀ приложено вдоль оси z, магнитный момент согласно классической физике приобретает энергию

,                                            (1.8)

где  проекция  на ось z. Квантовый аналог выражения имеет вид

                                                        (1.9)

В этой ситуации имеется 2I + 1 невырожденных энергетически уровня, соответствующих 2I + 1 возможным значениям . Ядерный магнитный резонанс будет наблюдаться на частоте

                                                (1.10)

Правила отбора для рассматриваемых переходов . Поэтому

                                                         (1.11)

В качестве примера на Рисунке 1 представлено расщепление уровней энергии для ядра со спином ½ в магнитном поле. Обычно магнитные поля в современных спектрометрах 1.5–12 Т (15–120 КГс). Это соответствует частотам десятки и сотни МГц, т.е. радиочастотному диапазону спектра.

2. СПЕКТРЫ ЯМР И ИХ ИНТЕРПРЕТАЦИЯ

Мы ограничимся кратким рассмотрением данных протонного магнитного резонанса (ПМР), когда в качестве резонирующих ядер выступают ядра водорода ¹Н (протоны).

2.1. Химический сдвиг

Уравнение 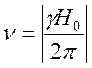, где  – константа для данного сорт ядер, не является вполне точным в виду того, что ядра в реальных образцах всегда окружены электронами, которые экранируют резонирующее ядро от действия внешнего магнитного поля Н₀. В результате поле, "чувствуемое" ядром, оказывается меньше H₀ на величину , где  – константа диамагнитного экранирования. По этой причине условием резонанса будет условие:

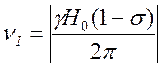,                                                     (2.1)

где  так называемый химический сдвиг, который рассчитывают по формуле

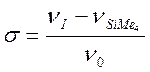                                                        (2.2)

где – частота резонанса для эталонного соединения SiMe₄, для которого хим. сдвиг  принимают за ноль,  – "рабочая" частота спектрометра.

Вследствие того, что масштаб изменения  относительно  составляет обычно только десятки и сотни герц, а рабочая частота спектрометра – десятки и сотни мегагерц, то оказывается, что величину  удобно выражать в безразмерных единицах, кратных коэффициенту 10⁻⁶. Легко видеть, что хим. сдвиг в таких единицах не зависит от применяемого внешнего поля. Величина 10⁻⁶ представляет собой миллионную долю (м.д.) от напряженности приложенного магнитного поля (или частоты спектрометра). В справочной литературе величины хим. сдвигов обычно указывают в м.д. Следует учесть, что определять хим. сдвиг как разность - можно только в том случае, когда эталонное вещество находится в растворенном виде в самом образце (внутренний эталон). При другом методе работы (внешний эталон: эталон и образец не находятся в одном и том же растворе) следует вводить поправку на разницу объемных магнитных восприимчивостей жидкостей, причем поправка зависит от формы ампул и от ориентации последних в магнитном поле H₀.