ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”, страница 19

                                       (9.7)

где Р – вероятность нахождения СНСl₃ в комплексе Сr(асас)₃·СНСl₃, а Dn_1/2P и Dn_1/2S определяются соотношениями:

                                          (9.8)

                                                        (9.9)

В этих формулах  – ширина линии СНСl₃ в комплексе Сr(асас)₃·СНСl₃;  – вклад в ширину линии из-за случайных хаотических столкновений СНСl₃ с парамагнитным комплексом;  – ширина линии хлороформа без парамагнитного комплекса.

С учетом соотношений (9.8) и (9.9) выражение (9.7) можно представить в виде:

                                (9.10)

Для молекул, не взаимодействующих с парамагнитным комплексом (P = 0), соотношение (9.10) будет выглядеть как

                                         (9.11)

В качестве вещества, не образующего комплекса с Сr(асас)₃, могут использоваться вещества, применяемые в ЯМР в качестве эталонов – ТМС, циклогексан и др. Поскольку вероятности случайных столкновений СНСl₃ и инертного эталона с парамагнитным комплексом приблизительно равны, выполняется соотношение:

 » 

Кроме того, с достаточной точностью можно полагать, что в диамагнитных растворах ширины всех линий приблизительно одинаковы и

 » 

Обозначим разность наблюдаемой ширины линии СНСl₃ в присутствии Сr(асас)₃ () и ширины линии эталона в этом же растворе () как

                                 (9.12)

Тогда, вычтя выражение (9.11) из выражения (9.10), получим:

                                                     (9.13)

Вероятность нахождения СНСl₃ в комплексе Сr(асас)₃ определяется как отношение концентрации [ML] к концентрации свободного лиганда [L]. Принимая во внимание, что

,

на основании условия материального баланса

выражение (9.13) приводится к виду

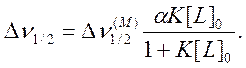                                      (9.14)

Здесь a = [M]₀/[L]₀, [M]₀ и [L]₀ – общие концентрации М и L. Так как a << 1, в уравнении (9.14) учтено, что [L] » [L]₀.

Таким образом, как видно из (9.14), константу устойчивости можно определить из анализа зависимости ширины линии СНСl₃ () от концентрации СНСl₃.

Методика проведения эксперимента и расчет величины константы устойчивости

1. Готовится раствор СНСl₃ и Сr(асас)₃ в ССl₄ с [СНСl₃] ³ 6 моль/л и a £ 0,01.

2. В ампулу ЯМР помещается приблизительно 0,6 мл исходного раствора с добавлением около 5% (объемных) эталона циклогексана.

3. Записывается спектр ЯМР образца, состоящий из двух линий (одна линия хлороформа, другая циклогексана) и измеряются ширины этих линий.

4. По формуле (9.12) вычисляется разность

5. Уменьшают концентрацию СНСl₃, добавляя в ампулу растворитель ССl₄, и вновь вычисляют . Таким образом, получают несколько (5‑10) точек зависимости  = f([CHCl₃]).

6. На основании уравнения (9.14) строят линейную зависимость 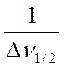 от 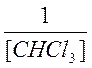 и по методу наименьших квадратов вычисляют значения К и . Результаты заносят в таблицу.

	[CHCl3]	1/	1/[CHCl3]

7. Результаты обрабатывают по МНК, вычисляя величины стандартных отклонений  и  на основании общих выражений (9.4)-(9.6),

p = 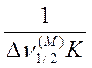;                                     q = ;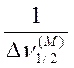

                     

;                       

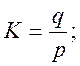
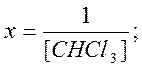
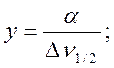
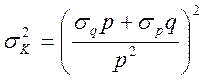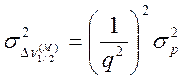
Результаты заносят в таблицу

P	q	sp	sp	K	sK

ЛАБОРАТОРНАЯ РАБОТА Я-3

Определение величин изменения энтальпии и энтропии для реакции внешнесферной координации метиленхлорида к бипиридинату бис(ацетилацетоната) кобальта(II) (Со(асас)₂Ру₂)

При добавлении СН₂Сl₂ к раствору Со(асас)₂Ру₂ происходит образование нового комплекса согласно реакции

      К