ЯМР спектроскопия: Методическое пособие к практикумам “Химическая термодинамика” и “Химическая кинетика”, страница 7

Компоненты намагниченности во вращающейся системе координат в плоскости, перпендикулярной , обозначим  и , где  – компонента в направлении , т.е. ,  – компонента вдоль оси .

                                        (3.7)

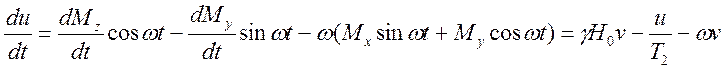. (3.8)

 может быть найдено аналогично.

Уравнения Блоха во вращающейся системе координат имеют вид

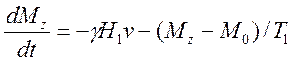
                                                         (3.9)

,

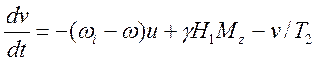где .

3.3. Стационарный эксперимент

В обычном стационарном эксперименте детектируется компонента намагниченности , фаза которой сдвинута на 90° по отношению к полю . В стационарном ЯМР спектрометре  медленно проходит через резонансное значение и сигнал непрерывно детектируется. При этом в каждый момент регистрации спектра выполняются условия стационарности. Стационарные значения ,  и определяются из уравнений Блоха для вращающейся системы координат при условии 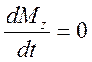, , 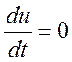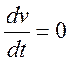. Несложно рассчитать, что тогда

,

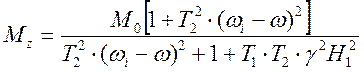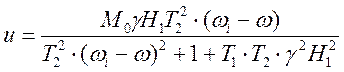                                  (3.10)

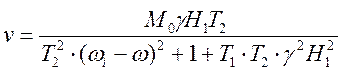
Аналогичные выражения в единицах частоты могут быть получены при замене , . Рисунок 8 показывает форму сигналов  и , которая следует из уравнений Блоха при условии  << . Это условие означает, что  не изменяет существенно разности заселенностей уровней рассматриваемого перехода. Сигнал поглощения  пропорционален

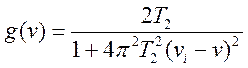,                                     (3.11)

 – форма линии.

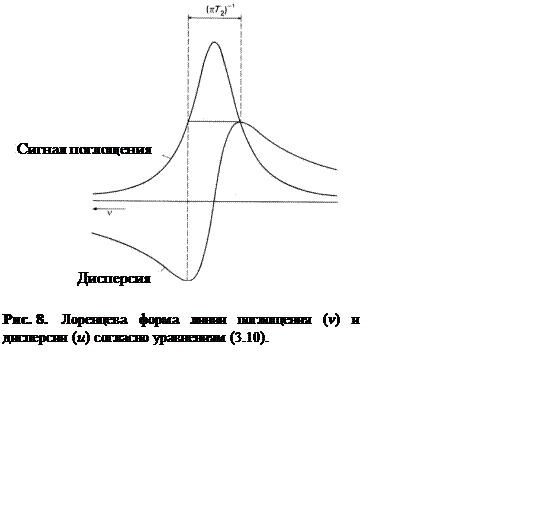Ширина на полувысоте линии поглощения равна  в единицах частоты,  – Лоренцева форма линии.

Лоренцева форма линии будет наблюдаться в случае, когда релаксация  и  строго экспоненциальна с единственным значением . На практике линии в ЯМР-эксперименте часто не имеют лоренцевой формы и даже асимметричны. Это связано с тем, что естественная ширина линиймала по сравнению с наблюдаемой шириной, обусловленной, например, неоднородностью магнитного поля по объему образца. Наблюдаемую ширину линии обозначим .

3.4. Импульсная ЯМР-фурье спектроскопия

При достижении резонанса во вращающейся системе фиктивное поле, обусловленное вращением, полностью компенсирует поле , направленное вдоль оси , так что с  взаимодействует только поле , лежащее в плоскости ху. Поскольку  вращается с той же частотой, что и система координат, то можно произвольно предположить, что  направлено вдоль вращающейся оси . Под действием   будет прецессировать вокруг  в плоскости .

Рассмотрим поведение спиновой системы, подвергнутой воздействию ВЧ-импульса. Будем считать, что ВЧ от передатчика включается и выключается так быстро, что огибающая ВЧ-колебаний во время импульса имеет прямоугольную форму. Примем также, что длительность импульса  мала по сравнению с  и , так что релаксация за время  не происходит. Из уравнения Лармора (ω = ) следует, что угловая частота прецессии относительно оси  равна . Угол , на который повернется М в ходе прецессии за время , дается выражением

                                                   (3.12)

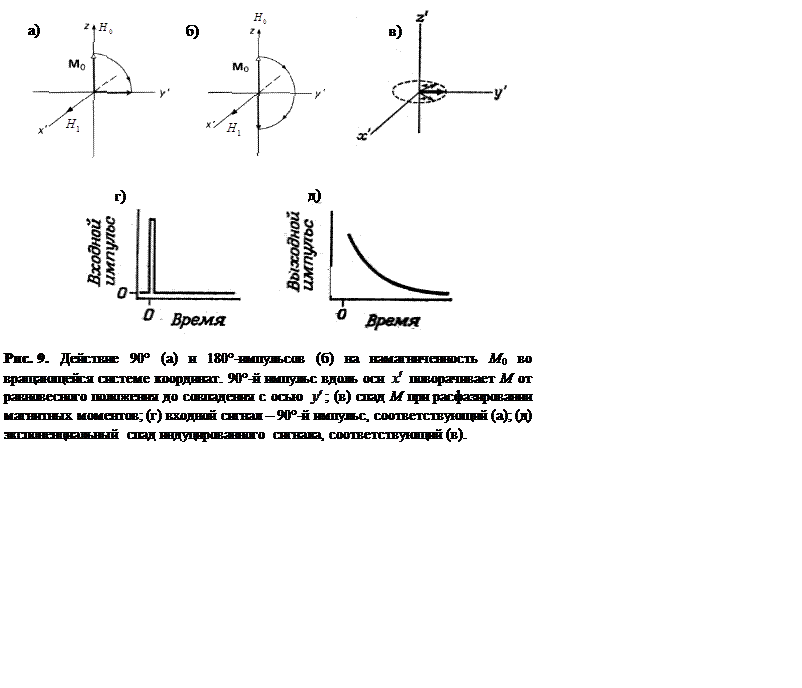
Это основное соотношение для применения импульсных методов. Величина , при которой  называется 90°-м импульсом, величина , при которой  – 180°-м импульсом (Рисунок 9).

Пусть вдоль оси  в системе координат, вращающейся с частотой ВЧ‑поля, приложен 90°-й импульс. По окончании импульса намагниченность  направлена точно по оси , (Рисунок 9а). Как уже отмечалось, устройство спектрометров ЯМР таково, что интенсивность наблюдаемого сигнала определяется скоростью изменения намагниченности в плоскости . Этот наведенный сигнал называют сигналом свободной индукции, поскольку его наблюдают после окончания 90°-го импульса, т.е. в отсутствии приложенного ВЧ‑поля. В отсутствие релаксации в неподвижной лабораторной системе координат после 90°-го импульса наблюдалось бы вращение  с частотой  в плоскости ху. По мере развития поперечной

релаксации сигнал уменьшается (см. Рисунок 9в).