Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 8

  Плотность теплового потока на единицу поверхности с ростом радиуса уменьшается.

- коэффициенты теплопередачи, отнесённые к поверхности 1 или 2.

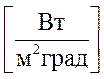
Существует понятие тонких цилиндрических стенок.

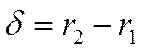  Возьмём  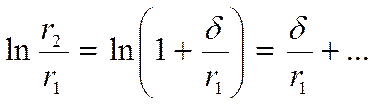где

  Если 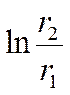можно с достаточной точностью представить как первый член разложения, то это тонкая стенка.

  Для тонких стенок выражение для полного количества тепла. передаваемого через цилиндрическую стенку может быть записано в следующем виде.

         (*)

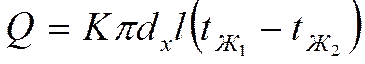  Причём К рассчитывается как для плоской стенки а диаметр d_x берётся по стороне с наименьшим коэффициентом теплоотдачи. Если коэффициенты теплоотдачи близки друг другу то расчётный диаметр является средним арифметическим:

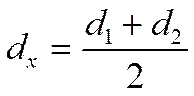
  Докажем это:

Учитывая, что для тонкой цилиндрической стенки 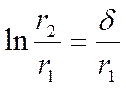, запишем:

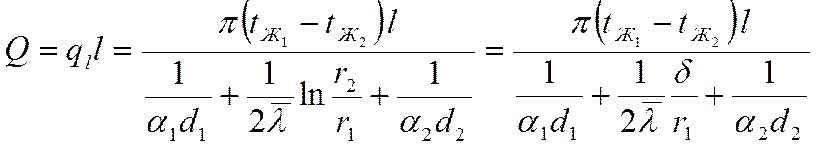
Если стенка тонкая, то мы можем предположить, что , то есть:

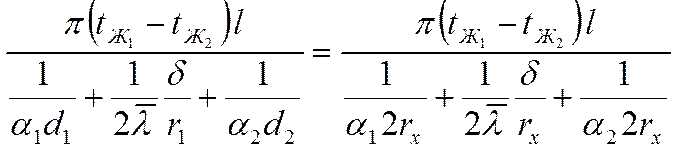
Преобразуем знаменатель, вынося за скобки :

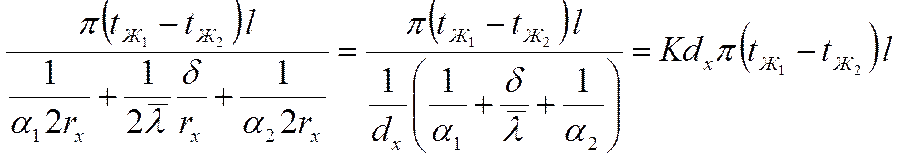
Справедливость выражения (*) для цилиндрической тонкой стенки доказана.

Температурное поле в пластине (бесконечной плоской стенке) с внутренними источниками тепла.

 

                                     Будем считать, что - известно,

 

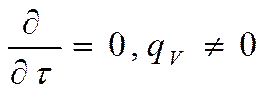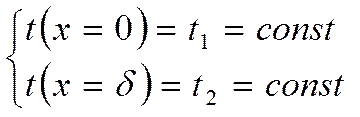
- изотропные источники (равномерно распределённый по стенке),        = const, не зависит от координаты.

                  ;                                   ;

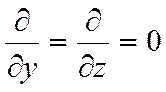
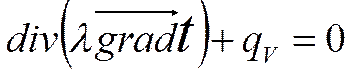
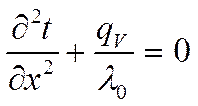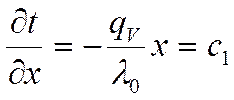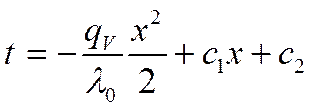
Воспользуемся граничными условиями:

                                  ^x=0

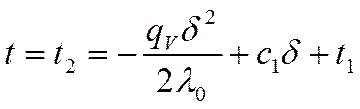
x= d:

                   _x=d            

Отсюда:

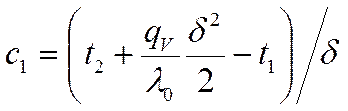
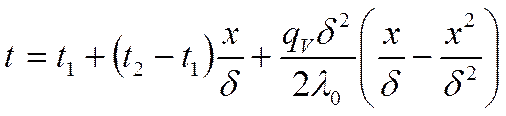
Будем предполагать, что экстремум функции существует в точке

         

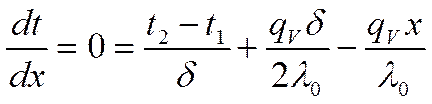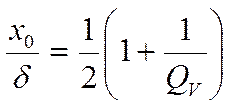
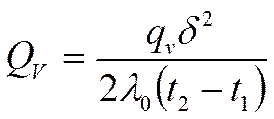
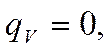
1.   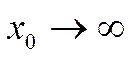                                 (экстремума нет)

2.                               

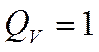
3.                               

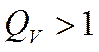
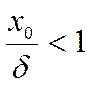
4.                          

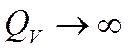
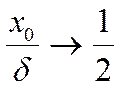
Если пластину делим серединной плоскостью, то существование экстремума в левой полуплоскости невозможно!!!

Температурное поле в круговом цилиндре с внутренними источниками тепла.

  Дан цилиндр бесконечной длины радиусом

Задано: на внешней поверхности:

      

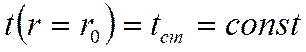
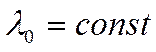
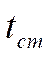не зависит оти

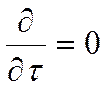  - условие стационарности.

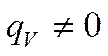  - наличие внутренних источников тепла.

Условие 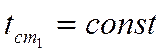 переводит задачу в класс одномерных задач, если источники изотропные (равномерно распределены).

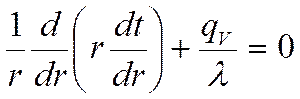   (1)       - уравнение теплопроводности.

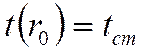   - граничные условия.

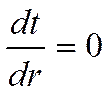    (2)        - условие симметрии.

  Условие симметрии – постоянство градиента исследуемого параметра в точке симметрии (независимость градиента от направления).

   Ноль в выражении (2), потому что отвод тепла осуществляется в окружающую среду.

  Проинтегрируем выражение (1):

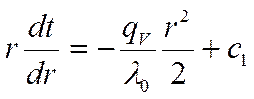
Из условия симметрии, при          

Разделим полученное выражение на и проинтегрируем:

                                                                                                   

                                                                           

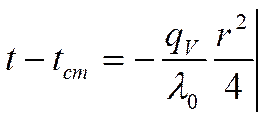
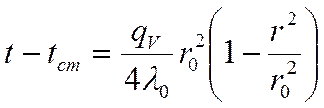             - квадратичная функция.

Изобразим эту параболу:

 

 

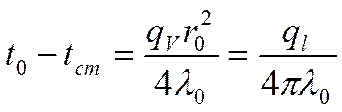Температурное поле цилиндрической стенки с внутренними источниками тепла.

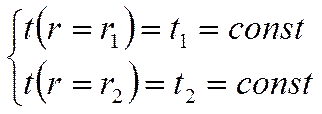Заданы: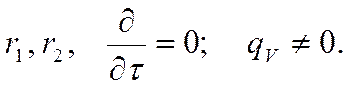 

        

Задача одномерная

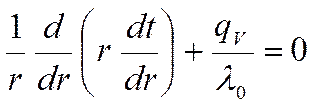
Умножим это выражение на и проинтегрируем:

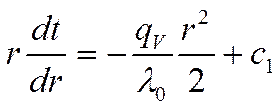
Умножим на 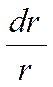и проинтегрируем второй раз:

 (*)

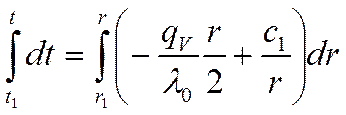
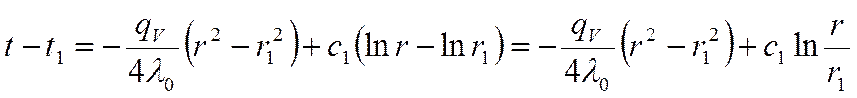Найдем , используя граничные условия:

               

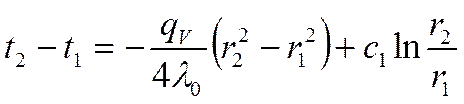
Отсюда равно:

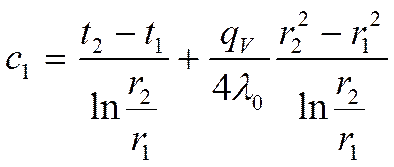
Подставим это выражение в выражение (*), получаем:

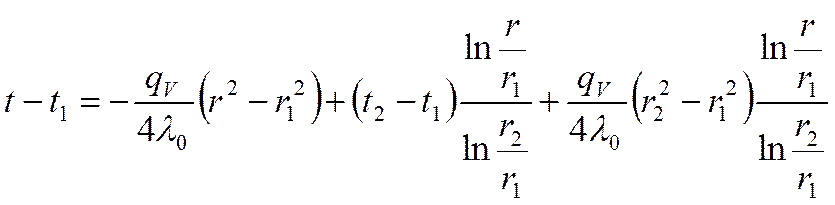
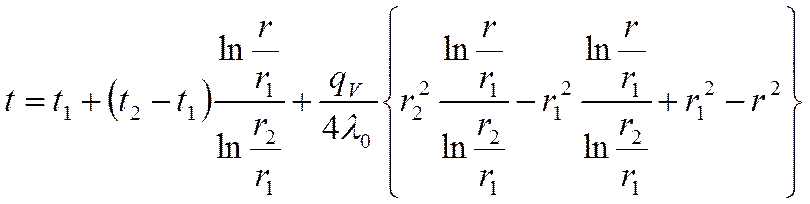
Учитывая, что: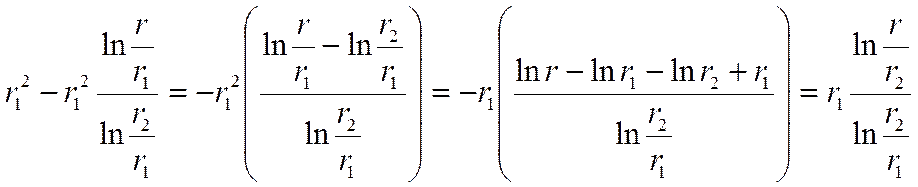

окончательно получаем выражение для температурного поля в бесконечной цилиндрической стенке с внутренними источниками тепла:

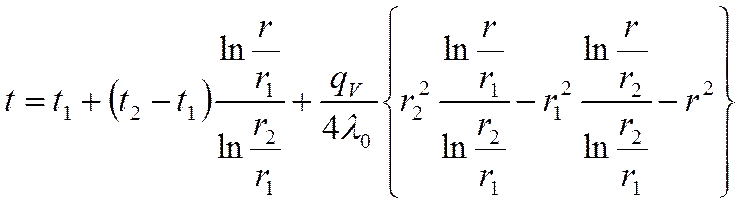
Возьмём производную:

где - точка экстремума:

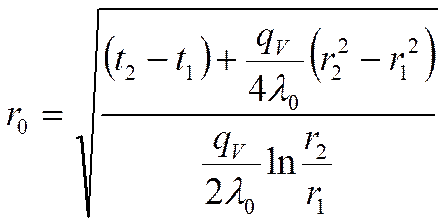
Критический диаметр цилиндрической стенки. Выбор тепловой изоляции.