так же известны.
![]()
![]()
![]() - могут отличаться
- могут отличаться
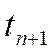
![]() друг от друга, т. к. пластинки
друг от друга, т. к. пластинки
могут быть из разных материалов.
0 x
n
Свойства любого слоя постоянны по осям xиz.
Решая соответствующие уравнения теплопроводности, мы получим:
 ;
;
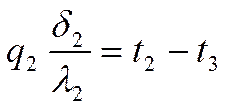 ;
…
;
… 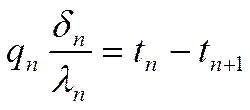
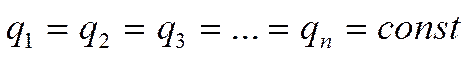
Плотности теплового потока по оси х согласно нашему условию есть величина постоянная и на границе не может быть скачка согласно закону сохранения.
Просуммируем:
![]()
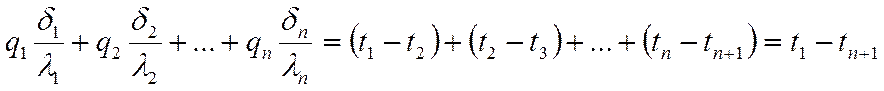
так как величина 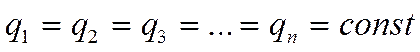 , вынесем её за скобки:
, вынесем её за скобки:
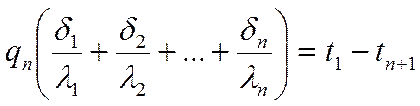
Разделив на выражение в скобках обе части, получаем:


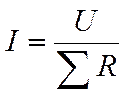

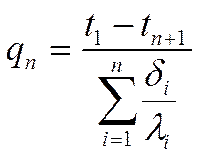 по аналогии
по аналогии
термическое сопротивление
![]() - индекс
слоя. многослойной стенки.
- индекс
слоя. многослойной стенки.

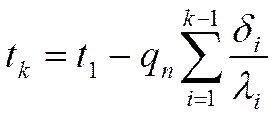 Заменим n+1 на k:
Заменим n+1 на k:
Заменим 1 на k: на границе по ходу -
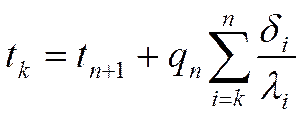 - слева или справа.
- слева или справа.
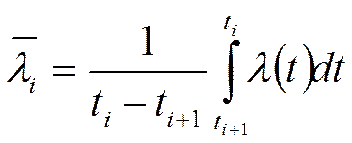
Найдём температурное поле в плоской стенке.
Вернёмся к уравнению теплопроводности после первого интегрирования:
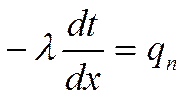
а)Пусть ![]() ; проинтегрируем:
; проинтегрируем:
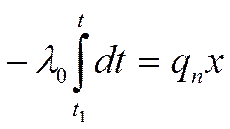
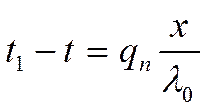
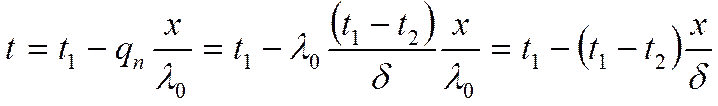
Температура в i – том слое:
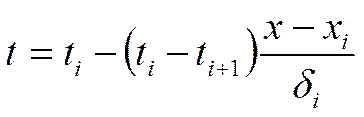
б) ![]() Для
переменного значения l:
Для
переменного значения l:
Пусть 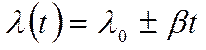
Проинтегрировав это выражение, получим:
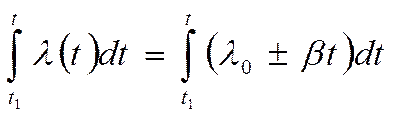
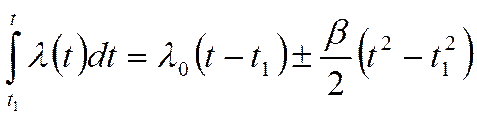
![]()
![]()
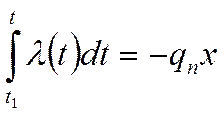
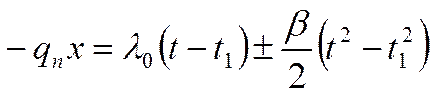
Умножим обе части уравнения
на ![]() :
:
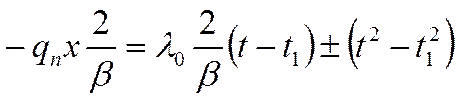
Раскроем скобки:
![]()
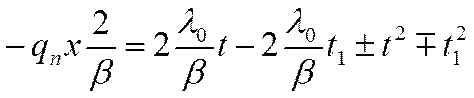
Прибавив и отняв 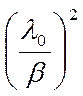 от правой части уравнения, получим:
от правой части уравнения, получим:
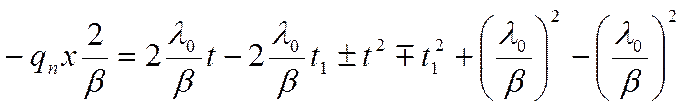
Рассмотрим два случая:
1) 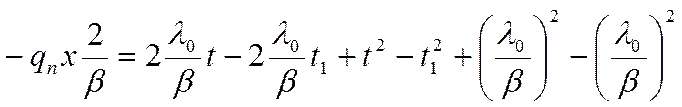
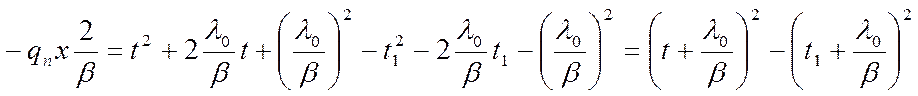 Откуда
t равно:
Откуда
t равно:
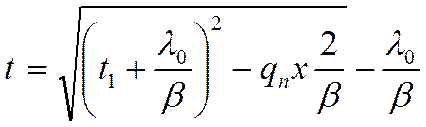
2) 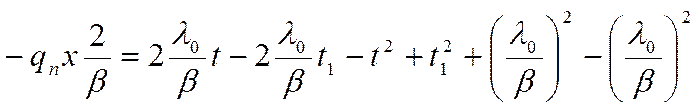
В этом случае:
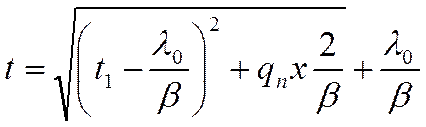
Объединяя эти два случая, получим решение нашей задачи:
![]()

 t1
t1 ![]()
![]() +b
+b 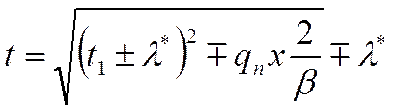
![]() t2 где
t2 где 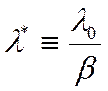
-b
Температурное поле и плотность теплового потока в цилиндрической стенке.
r1 Заданы: r1, r2 ; l(t)
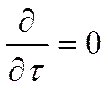
![]()
![]()
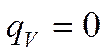 r2 ; ;
r2 ; ;
![]()
![]() z t1
z t1
По координате zцилиндрическая стенка
![]() t2 бесконечна.
t2 бесконечна.
Заданы граничные условия первого рода:
![]()
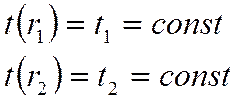 Все температуры по длине цилиндра
= const
Все температуры по длине цилиндра
= const
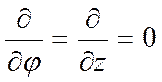 -
задача превратилась в одномерную.
-
задача превратилась в одномерную.
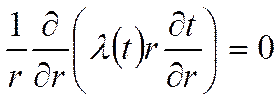
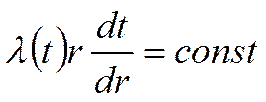
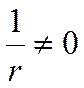 Это условие вместе с граничными условиями есть математическая
постановка задачи.
Это условие вместе с граничными условиями есть математическая
постановка задачи.
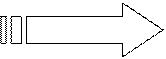 |
Так как ;
Рассмотрим два геометрических тела:
1) Сплошнойцилиндр:
 |
|||
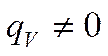 |
|||
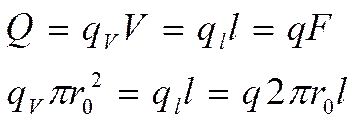 |
где r0 – радиус цилиндра.
 |
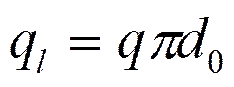
2) Цилиндрическая стенка без внутренних источников тепла:
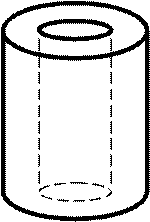 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.