Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 24

 - молекулярный коэффициент теплопроводности;

- турбулентный аналог коэффициента теплопроводности, определяется молярным механизмом теплообмена.

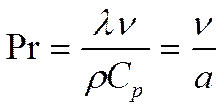
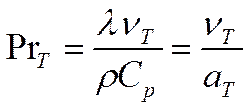
        Pr_T – турбулентный аналог числа Прандтля.

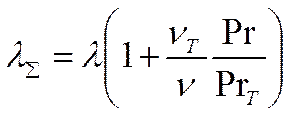
Пусть .

         (*)

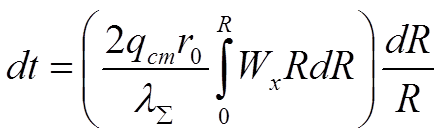          Средневзвешенная температура через безразмерные величины:

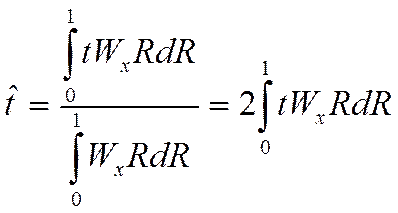
Будем интегрировать по частям: в нашем случае  

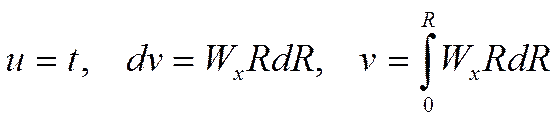
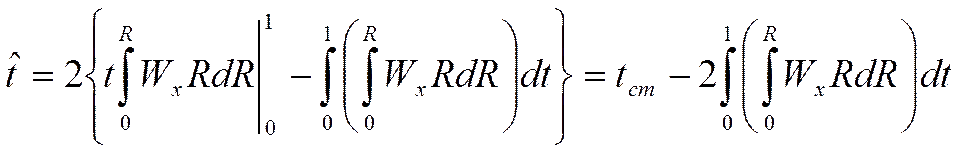          Учитывая, что dt=(*), получаем:

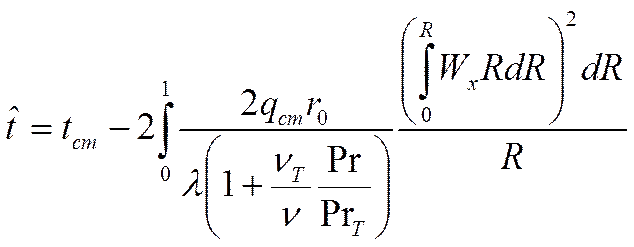
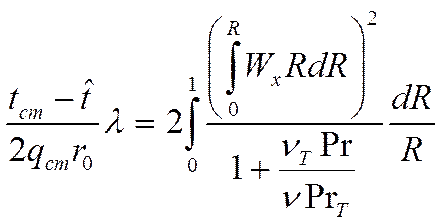
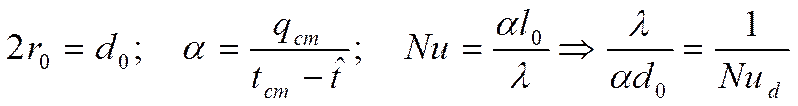
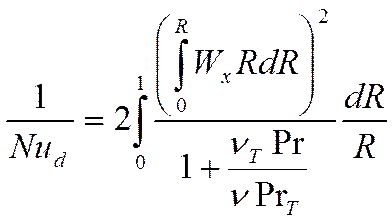
это классическая форма записи соотношений параметров для стабилизированного течения или интеграл Лайона.

Профили скорости при стабилизированном течении жидкости в трубе.

а) Рассмотрим ламинарный режим течения: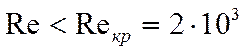

          Для этого режима характерен квадратичный профиль скорости:

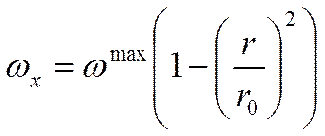
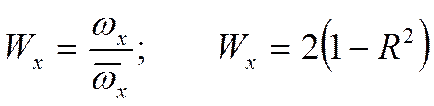
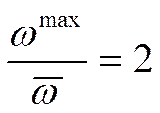   - для любых квадратичных течений.

          Для ламинарного режима течения 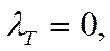 тогда:

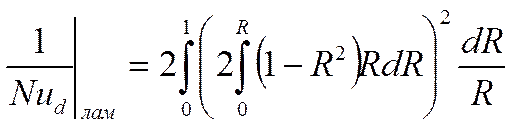
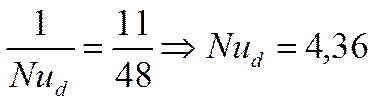   - ответ на нашу задачу при ламинарном режиме течения, если течение стабилизировано и .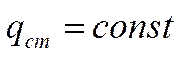

Условие 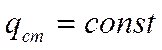 не у всех стенок выполняется.

Если в качестве граничных условий принято,  то мы получим немного другое решение:

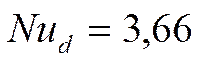
б) Рассмотрим турбулентный режим течения.

Турбулентный поток в трубе принято разделять на подслои:

1)  Вязкий подслой:

В вязком подслое профиль скорости характеризуется следующим соотношением:

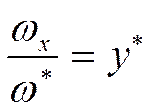
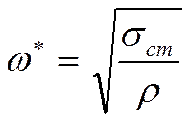   - динамическая скорость.

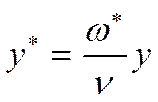   - универсальная безразмерная координата.

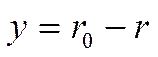       - координата, отсчитываемая от стенки.

Вязкий подслой существует, если .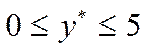

2)  Буферный подслой:

Существует при значении .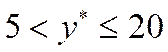

3)  Развитое турбулентное ядро:

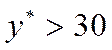
          Для второго и третьего подслоя в профиль скорости выражается одной формулой:

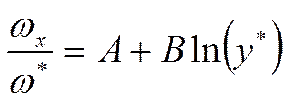
	А	В
	3,05	5,0
	5,5	2,5

В вязком подслое – линейная зависимость, в остальных – логарифмическая.

Расчёт интенсивности теплообмена при турбулентном течении жидкости в трубе.

          Опытными данными была получена следующая зависимость:

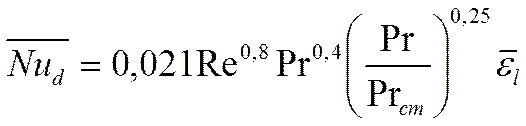
Это формула Михеева.

          Эта формула возникла не на пустом месте. Похожая зависимость была получена в прошлых лекциях для плоской пластины из пропорциональности:

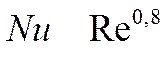
Формула Михеева рекомендуется для следующего диапазона параметров:

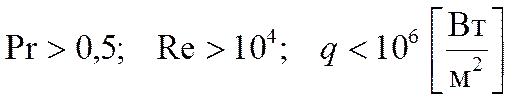
          За границей параллельно была получена формула:

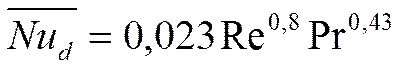
это формула Диттуса-Белтера.

Все физические параметры, входящие в  берутся по средневзвешенной температуре, а  берётся при температуре стенки.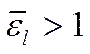

График изменения  по длине трубы:

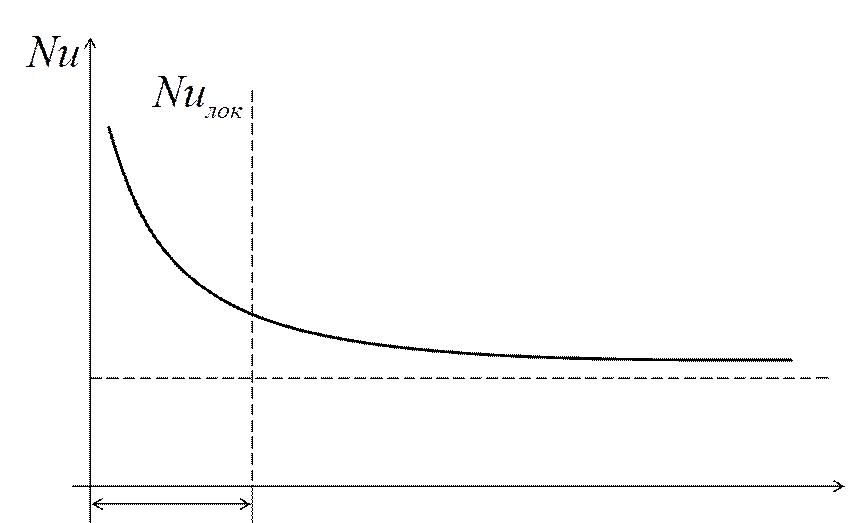
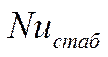
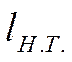
        Если 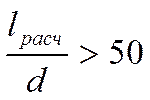, то . Если 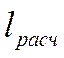 меньше чем 50 калибров, то  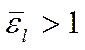берётся по таблицам. Для короткой трубы рекомендуется считать не  среднее, а  локальный:

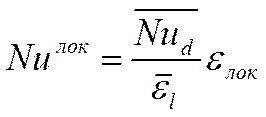
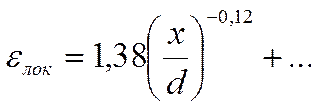
Эта зависимость длинная, но если 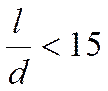, то можно ограничиться одним членом. 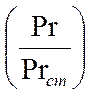 - учёт изменения теплофизических параметров среды от температуры в пристенном слое.

        Под руководством Петухова получена формула, подтверждающая интенсивность теплообмена с учётом трения трубы:

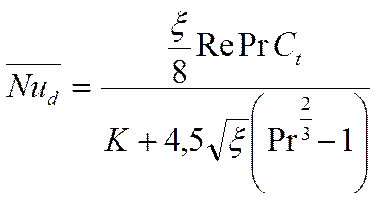
 - аналог коэффициента трения

        Для турбулентного режима течения:

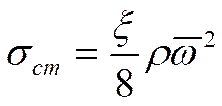
         - поправочный множитель, имеющий такое же значение, что и отношение :

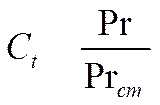
        Сам Петухов давал следующие значения:

для жидкости: 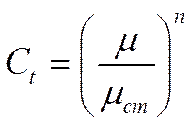      n= 0,11 – нагрев; n= 0,25 – охлаждение.

для газов: 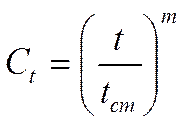  m = 0 – нагрев; m = (0,3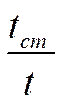+0,36) – охлаждение

        Он так же рекомендует формулу Филоненко для вычисления коэффициента трения:

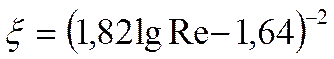
        В уравнении Петухова коэффициент К равен:

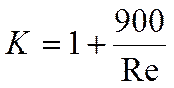
а поскольку формула Петухова справедлива при , то . И если Pr = 1, то в формуле остаётся один числитель.

Расчёт интенсивности теплообмена в шероховатых трубах.

Замечание: все соотношения в справочниках относятся к теплообмену и гидравлике технически гладких труб – поверхность трубы соответствует гос. стандарту. В целом, шероховатость улучшает теплообмен, но ухудшает гидравлику. Можно отметить два момента:

1)  Если режим течения ламинарный, то влияние шероховатости на интенсивность теплообмена пренебрежимо мало, поскольку режим передачи тепла – молекулярный.

2)  При турбулентном режиме с увеличением шероховатости интенсивность возрастает. Сильное влияние оказывает величина . При очень малых , что характерно для жидких металлов, основным механизмом передачи тепла является теплопроводность вне зависимости от режима течения. Следовательно, для таких сред шероховатость на интенсивность теплообмена влияет слабо.