Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 16

                проекция скорости на ось x      проекция на ось у     проекция на ось z

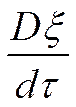 - субстанциальная производная от параметра, которая учитывает изменение параметра по времени с учётом перемещения центра объёма.

        Существует понятие массовых (объёмных) сил – это реально существующие силы. Примером таких сил является тяготение, инерция, магнитное поле, электрическое поле, биополе.

        Вводится понятие поверхностных сил. Они не существуют, но начинают проявляться только тогда, когда в движущуюся среду вводится возмущающий объект (стенка). Мы можем их рассматривать как силы, проявляющиеся как действие на поверхность этого тела. Примеры поверхностных сил: давление и силы трения.

        Математическое определение: плотностью распределения массовых сил называется предел отношения вектора 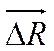 к массе  при стягивании объекта в точку:

            

 

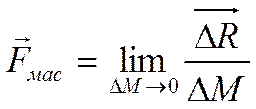
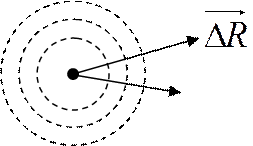
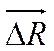         - главный вектор массовых сил, приложенных к объекту .

        Касательными силами на единицу поверхности называется вектор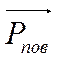

               

 

  

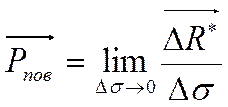
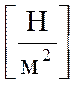
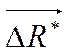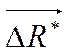
                                                                             - элементарная площадка

-  равнодействующая всех сил,

действующих на эту площадку.

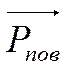        называется напряжением.

Массовые силы образуют векторное поле, так как в конкретной точке имеют одно направление и одну величину.

Поверхностные силы образуют тензор – бесконечное множество векторных полей. Тензор зависит от расположения площадки в точке.

        Рассмотрим текучую среду в декартовых координатах:

 

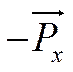
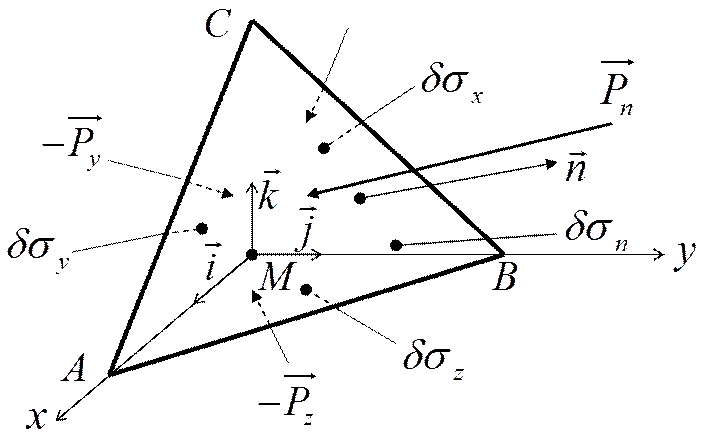        Рассмотрим жидкий тетраэдр МАВС. Основание – треугольник АВС, вершина – точка М.  - нормаль к площадке АВС.

В механике жидкостей и газов различают лицевую сторону площадки (от которой возведена нормаль) и внутреннюю сторону. Сила, действующая на лицевую сторону – плюсовая сила. Рассмотрим силы, действующие на все площадки: .

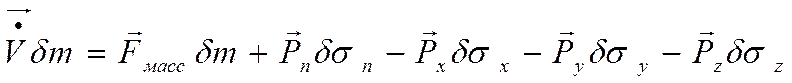
        Мы учли, что кроме поверхностных сил могут действовать массовые силы.

        - масса тетраэдра.

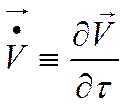          - ускорение (производная скорости повремени).

Начнём стягивать объект в точку: 

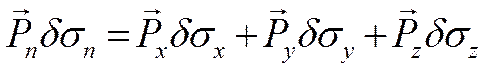
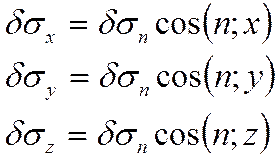
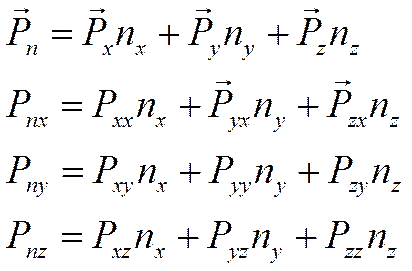
Эти девять проекций определяют .

        Проекции на оси координат напряжения, приложенного к любой наклонной площадке, выражаются линейно через проекции напряжений, приложенных к трём взаимно перпендикулярным плоскостям, лежащих в координатных плоскостях, то есть совокупностью девяти величин.

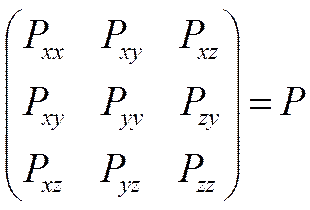
Эта матрица является тензором второго ранга.

  

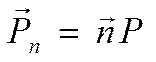
                                                                               Напряжённость.

Запишем относительно тензора второго ранга следующее:

        Отдельные компоненты тензора зависят от выбора направлений осей координат, но тензор в целом представляет физическую величину, выражающую состояние среды в данной точке и не зависит от выбора направлений осей координат.

        В любой точке может быть любой количество напряжений, в зависимости от направления площадки.

        Скорость любой точки твёрдого тела можно представить как скорость поступательного движения и угловую скорость вращения вокруг этой точки. Для жидкой среды появляется третья компонента – скорость деформации. Итак, скорость движения жидкости можно представить как скорость прямолинейного движения, скорость углового вращения и скорость деформации. Скорость деформации есть тензор, и соответствующие компоненты записываются так:

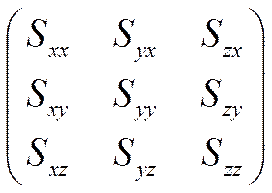
        Особенностью этой матрицы является то, что она симметрична в отличие от матрицы напряжений. Это значит, что если взять диагональ, то величины 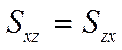.  Любой компонент этой матрицы рассчитывается очень просто:

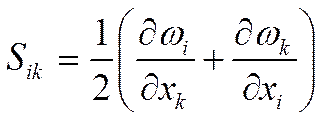
где: и означает координату. Например:

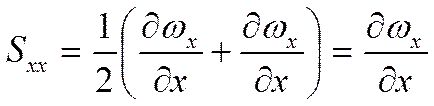
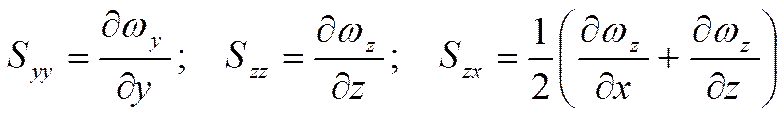
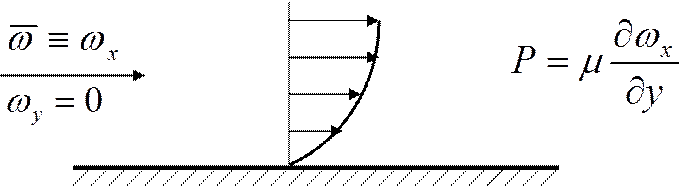
        Согласно гипотезе Ньютона-Стокса существует связь следующего вида:

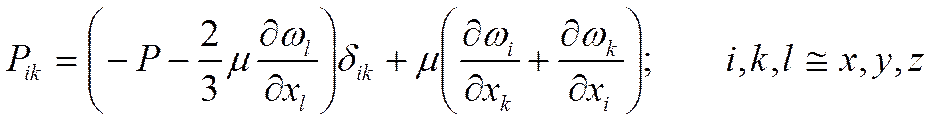
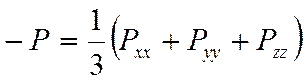 - является величиной, которая называется давлением среды. - дельта функция, ненулевая в одной точке:

 

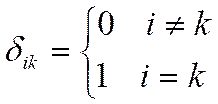
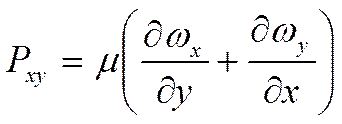
Вывод дифференциальных уравнений конвективного теплообмена

Уравнение неразрывности.