![]()
![]() эпюра
эпюра
![]()
![]()
![]() x
x
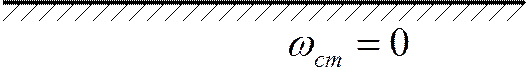 |
 Ньютон принимал гипотезу «прилипания». Он
предположил, что плотность поверхностных сил (касательные силы на единицу
поверхности) пропорциональны градиенту скорости
Ньютон принимал гипотезу «прилипания». Он
предположил, что плотность поверхностных сил (касательные силы на единицу
поверхности) пропорциональны градиенту скорости 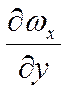 в перпендикулярном
направлении движения:
в перпендикулярном
направлении движения:
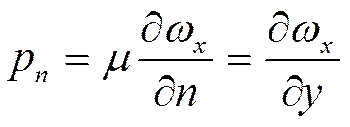
![]() -
касательные силы на единицу поверхности
-
касательные силы на единицу поверхности  .
.
![]() -
коэффициент динамической вязкости
-
коэффициент динамической вязкости 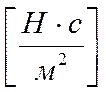 .
.
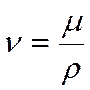 - коэффициент кинематической вязкости.
- коэффициент кинематической вязкости.
![]() -
параметр, характеризующий сжимаемость среды.
-
параметр, характеризующий сжимаемость среды.
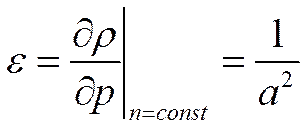 |
(причем постоянный
может быть любой параметр не зависящий от Р : ![]() …)
…)
![]() - скорость распространения малых
возмущений.
- скорость распространения малых
возмущений.
![]() - коэффициент температурного расширения
среды.
- коэффициент температурного расширения
среды.
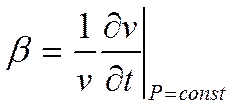
Если газ идеальный,
то 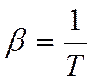 ;
;
Гипотеза прилипания работает не всегда. Это зависит от параметра Кнудсана:
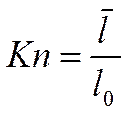
![]() - средняя длина пробега молекул до
соударения;
- средняя длина пробега молекул до
соударения;
![]() - характерный размер канала.
- характерный размер канала.
Для
сред , используемых в энергетике считается нормальным если ![]()
Если ![]() , то имеет место проскальзывание молекул и теория
прилипания лишь частично применима. Если
, то имеет место проскальзывание молекул и теория
прилипания лишь частично применима. Если ![]() - то гипотеза прилипания не работает.
- то гипотеза прилипания не работает.
Свободное течение – течение под действием объёмных сил (поле сил тяжести).
 |
|||||
Спецификой такого распределения является особое распределение скорости у стенки.

На некотором
удалении скорость будет близка к нулю – специфика свободного движения.
Существует некая зона основного изменения параметров ![]() .
.
Вынужденное движение:
![]()
 Градиент
температуры у стенки
Градиент
температуры у стенки
выше, чем при свободном
![]() движении.
движении.
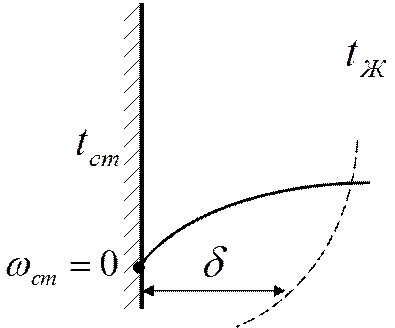
Стенка является возмутителем и температурного поля и скоростного.
Рассмотрим стеночку, вдоль которой течёт некая среда. Прандтль предположил, что существует некоторый слой переменной толщины – здесь будет основное изменение скорости.
 |
![]() - гидродинамический
пограничный слой.
- гидродинамический
пограничный слой.
![]() Прандтль
постулировал существование гидродинамического пограничного слоя с толщиной
Прандтль
постулировал существование гидродинамического пограничного слоя с толщиной ![]() . По аналогии с моделью Прандтля, Кружилин
предположил, что существует некий слой переменной толщины (тепловой пограничный
слой), в котором происходит основное изменение температуры.
. По аналогии с моделью Прандтля, Кружилин
предположил, что существует некий слой переменной толщины (тепловой пограничный
слой), в котором происходит основное изменение температуры.
 |
|||
 |
|||
Пути решения задач
Если математик предполагает, что система координат неподвижна, то можно по-разному оценивать изменение параметров в точке. В этом случае около точки выделяется объём с прозрачными стенками, который имеет неподвижный центр объема, и среда этот объём пронизывает.
 |
|||||||
![]()
![]()

![]() - локальный подход.
- локальный подход.
Локальный подход рассматривает локальную точку и некий условный объём
 определённая форма дифференциального уравнения.
определённая форма дифференциального уравнения.
Система координат привязывается к центру объёма. Этот локальный подход называется эйлеров подход. Если система координат подвижная, то такой локальный подход называется лагранжев подход.
Есть ещё один вариант, когда в пространстве с неподвижными координатами выделяется некий объём постоянной массы – субстанциальный подход.
![]()

![]()
![]() Мы
рассматриваем постоянную массу, но объём – переменный, границы этого объёма
деформируются
Мы
рассматриваем постоянную массу, но объём – переменный, границы этого объёма
деформируются![]() , центр объёма масс движется.
, центр объёма масс движется.
 |
Если
мы возьмём любой параметр ![]() , то изменение этого
параметра по времени нужно рассматривать как полную производную от сложной
функции:
, то изменение этого
параметра по времени нужно рассматривать как полную производную от сложной
функции:
![]()
![]()
![]()
![]()
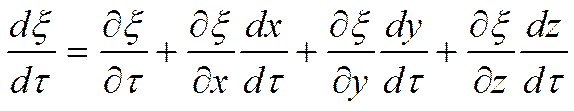
 |
|||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.