Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 3

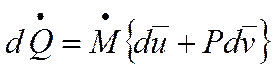
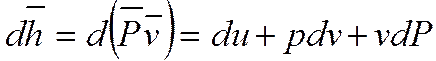
Получаем:                                                                         0

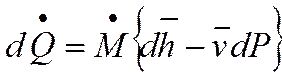
  Все последующие выражения справедливы для Р = const

Уравнение теплопроводности нельзя использовать, если внешние условия меняют внутренний состав твёрдого тела.

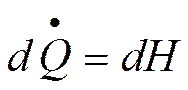                                                               где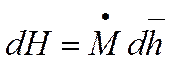

Рассмотрим процесс по времени и разложим H в ряд Тейлора вблизи точки t:

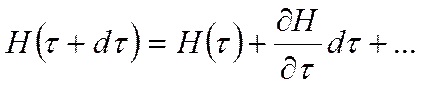
  тогда:

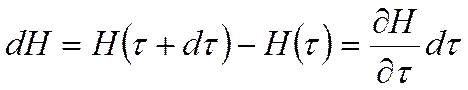
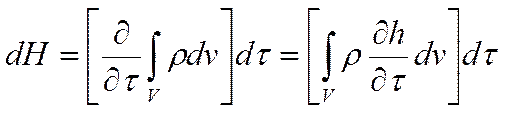
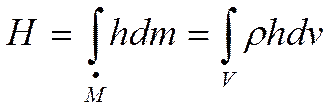
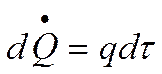
  Поток Qразобьём на две составляющие – на объёмную и поверхностную:

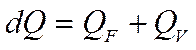
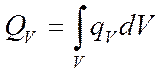  - объёмная генерация тепла.

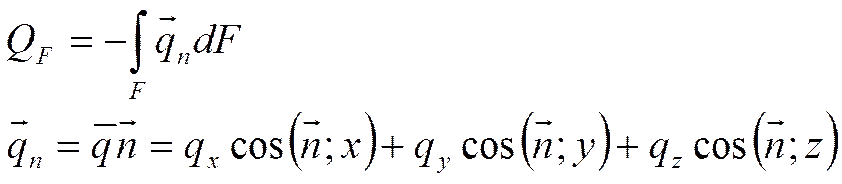
  По теореме Остроградского если есть некий вектор , то:

 

 

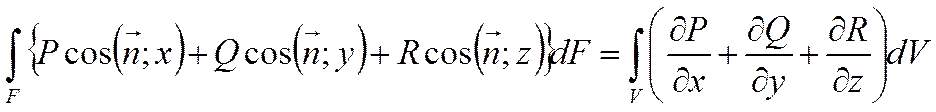
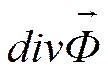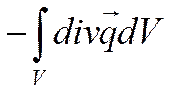Q_F   ^{По теореме Остроградского}   

  В конце концов, получим:

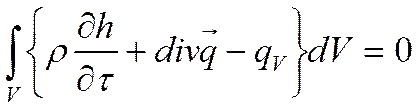
  Рассмотрим энтальпию как функцию двух независимых параметров – температуры и давления:              0  

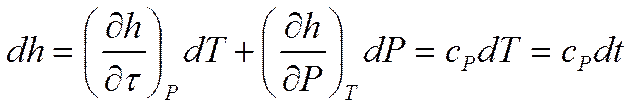
                с_P

  Предположим, что теплоёмкость по времени не меняется:

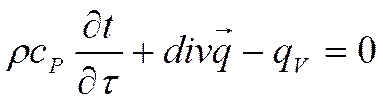
 Учитывая 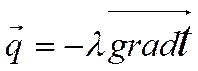,  окончательно записываем уравнение:

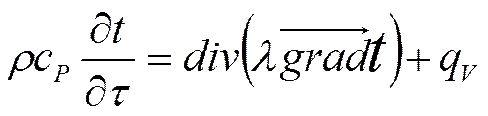
Это окончательный вид уравнения теплопроводности.

  Рассмотрим частный вид уравнения теплопроводности; если l = const, то её можно вынести за знак оператора дивергенции:

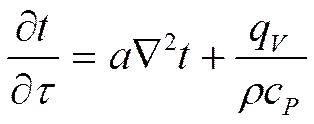    где:  

Классическое Уравнение Лапласа

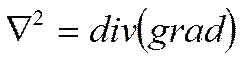
     (Если q_V  = 0)

Условия однозначности.

  Для того чтобы решить дифференциальное уравнение, необходимы условия однозначности. Их количество определяется порядком уравнения, а так же тем, является задача стационарной или нестационарной.

  Для стационарной задачи необходимы следующие условия однозначности:

1)  Задание формы и объёма области исследования.

2)  Начальные условия.

  Только для уравнений теплопроводности начальным условием является задание температуры как функции координатной области исследования, включая границу в фиксированный момент времени, который называется начальным моментом и обычно принимается за ноль.

  Математически это записывается следующим образом: если m есть совокупность координат точки области, то тогда начальное условие – есть поле температур для заданных координат:

                                                  (*)                 m V

t₀ =0 – точка отсчёта.

Не во всех задачах теплопроводности условие (*) задаётся именно таким образом. Иногда оно имеет вид:

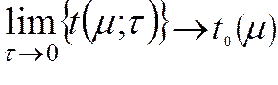
  Будем обозначать нестационарную задачу следующим условием:

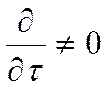                    ;              а стационарную -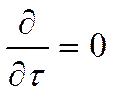           

  Условия однозначности включают и граничные условия нескольких типов (родов) – это есть задание температур или других параметров на поверхности, ограничивающей среду.

 Граничные условия первого рода – это задание температур на поверхности F:

                                       

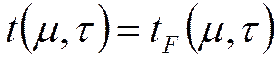
причём: ;   - произвольная.

  Если нет условий первого рода – задача решений не имеет.

Граничные условия второго рода – это задание плотности теплововго потока на поверхности:

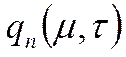
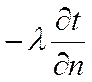                   по Фурье

                                                                                                                                               

                   F

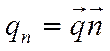- это поток для среды, нами изучаемой.

Граничные условия третьего рода формируется как задание непрерывности проекции плотности теплового потока на нормаль. Записывается это сочетанием закона Фурье и гипотезы  Ньютона-Рихмана:

                                                                                       

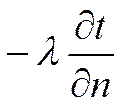
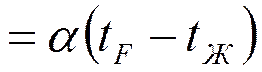
     q_n                                                                                         

                                                  _F

  Граничные условия третьего рода могут быть усложнены; если имеется изучаемая среда с высокой температурой (t>350⁰ C), то соответствующая среда имеет компоненту теплового излучения. Граничные условия IIIа в этом случае будут переписаны следующим образом:

 

                                                                                

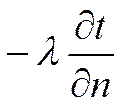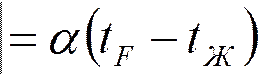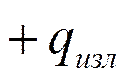                                          ^F