Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 17

                                                           Уравнение неразрывности мы будем выводить, используя локальный эйлеров подход. Будем использовать прозрачный для среды элемент постоянного объёма: .

Поток массы: 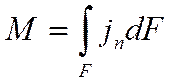          соответствующая площадь.

                                           плотность потока массы

                                                                         (*)

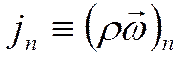
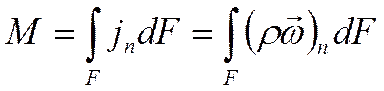
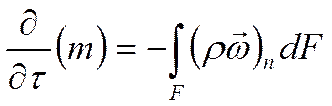
        Изменение массы в выделенном объёме по времени зависит от потока массы через поверхность.

Это закон сохранения массы в выделенном объёме:

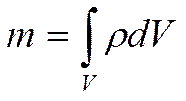
Преобразуем (*) по теореме Остроградского-Гаусса:

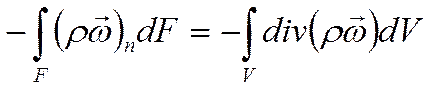
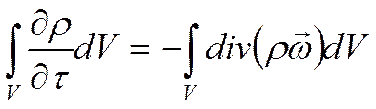
        Поскольку V произвольно, то это равенство возможно только при равенстве подынтегральных выражений:

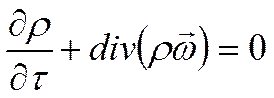
                                                           Это есть общее выражение закона сохранения массы или уравнение неразрывности.

Частный случай:

                                                           Несжимаемая среда .

пусть имеется плоское течение:

 

                                                                  

 

                                                       

 

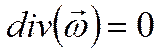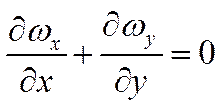Уравнение сохранения количества движения

        Рассмотрим субстанциональный подход, то есть около рассматриваемой точки мы исследуем макротело постоянной массы.

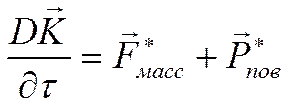   - обобщённый закон Ньютона.

        - главный вектор количества движения:

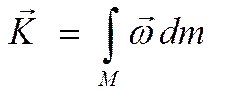
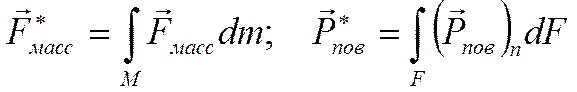
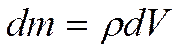
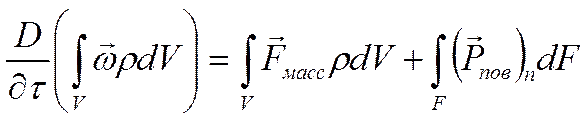
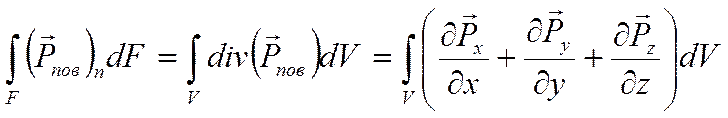
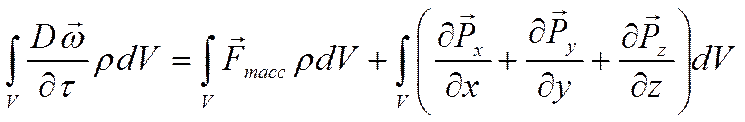
        В итоге получаем общее уравнение сохранения количества движения:

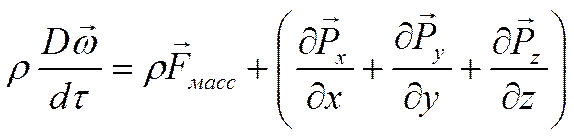
        Уравнение сохранения количества движения не может быть математически раскрыто, так как состоит из трёх уравнений, и мы должны перейти к проекциям.

Проекция на ось Х:

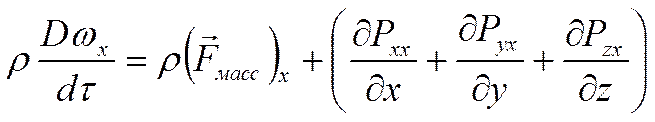
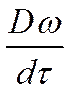 - производная особого рода.

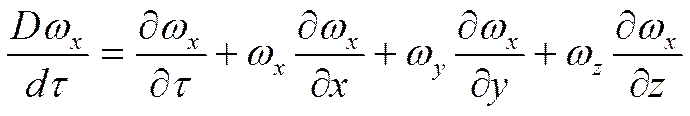
        Преобразуем 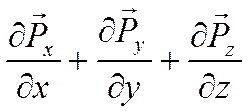, используя гипотезу Ньютона-Стокса по связи тензора напряжений и тензора деформаций:

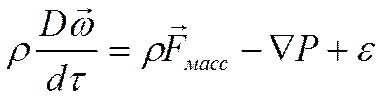
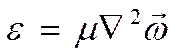        - учёт вязкости среды.

         - учёт давления перемещения частиц в соответствующем поле сил.

Проекция на ось Х:

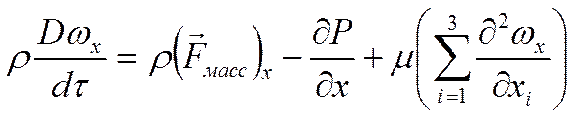
Совокупность уравнений, выражающих проекции на оси Х,У,Z, называются уравнениями Навье-Стокса.

Уравнение энергии

        Используем субстанциональный подход.

Обозначим: Е – совокупность внутренней и кинетической энергии тела:

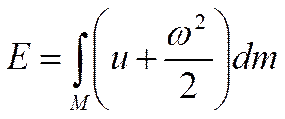
        Составляющую энергии потенциальную мы выделим отдельно как работу массовых сил:                                                I               II

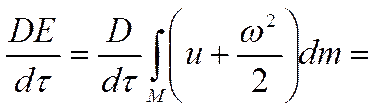  тепло  +   работа

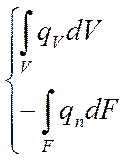        Разделим тепло внутренних источников и тепло, которое передаётся теплопроводностью или движением среды:

                                   - тепло внутренних источников.

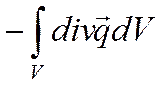
            I                    _{по Остроградскому}

II: Выделим работу массовых сил и поверхностных сил:

   работа массовых сил: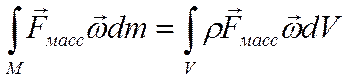

   работа поверхностных сил: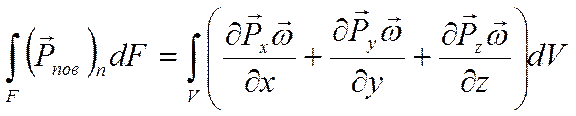

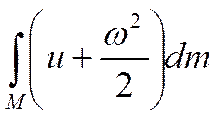  заменим на 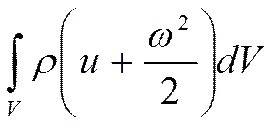, получим:

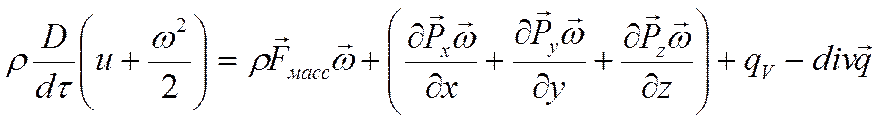   (а)

Домножим уравнение сохранения количества движения на вектор скорости:

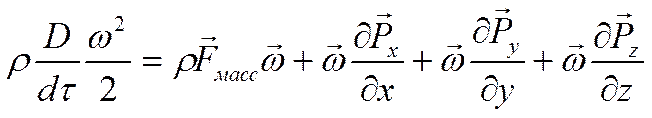                                (б)

Учитывая (б), из (а) получаем:

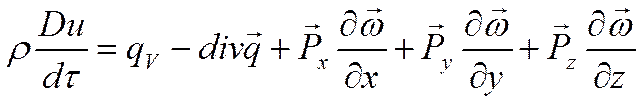
        Это общий вид уравнения энергии.

Преобразуем 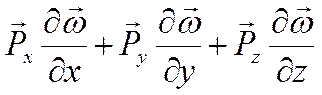, используя гипотезу Ньютона-Стокса:

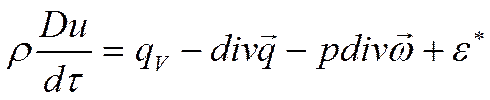
        - работа сил вязкости (работа касательных напряжений).

Обобщённый вид:

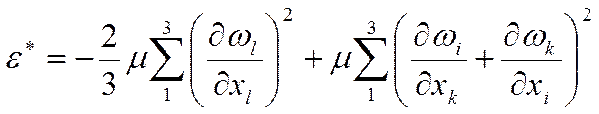
- работа сил сжатия (расширения) среды.

и на порядки больше чем , и на 3-4 порядка больше .

        Другая форма уравнения энергии.

Если мы сделаем замену: , мы получим:

                                                                                             (*)

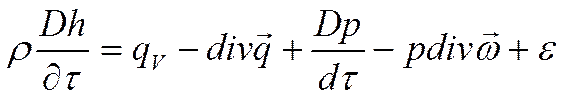
Если среда жидкая, то  (*) можно пренебречь для высокоскоростных потоков.

Запишем ещё один вариант – через энтропию:

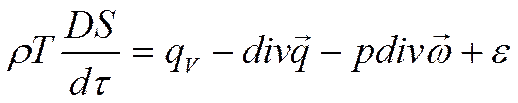
        Упрощённое представление: если мы представим 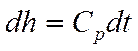 и пренебрежём (*), получим:

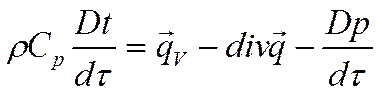
          Для безнапорных течений можно пренебречь , по Фурье 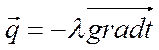, и если нет внутренних источников тепла, тогда:

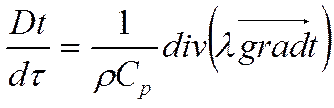
и если , получим:

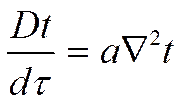
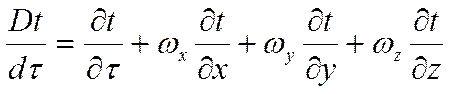
Однако такая запись уравнений не является общепринятой.

        Итак, любое описание явления с помощью дифференциальных уравнений преобразуется к описанию обобщённого случая, если выразить математическое описание в относительных (безразмерных) величинах. При таком переходе обязательно получаются безразмерные комплексы.