Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 6

                                    

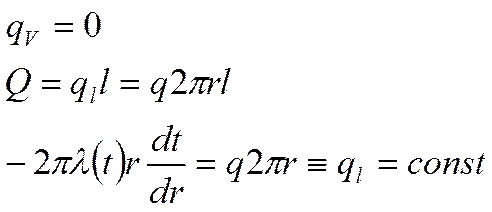
  В цилиндрической стенке линейная плотность теплового потока при граничных условиях первого рода и отсутствии внутренних источников тепла есть величина постоянная, не зависящая от координат.

 

     плоская стенка                                   

 

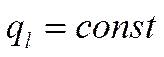     цилиндрическая стенка           

  Следствие: плотность теплового потока на единицу поверхности уменьшается при увеличении радиуса.

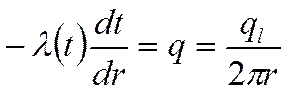            ;      проинтегрируем:

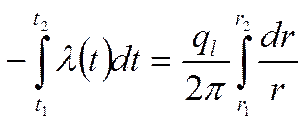                   умножим обе части на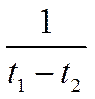

 

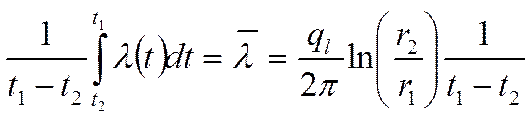
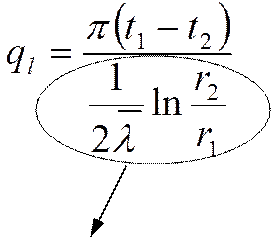Эта величина называется линейным                                         термическим сопротивлением

цилиндрической стенки.

R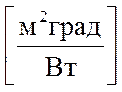                   R_l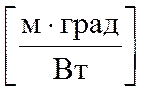

Линейная плотность теплового потока для многослойной цилиндрической стенки.

                                           ;          …          ;

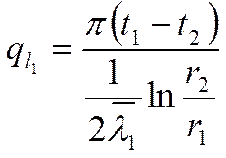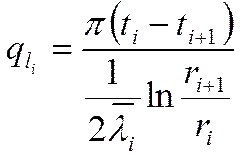так как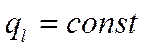                                                                             

 

                                                                    

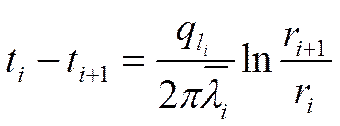
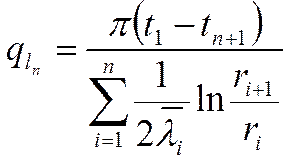полное линейное термическое сопротивление многослойной

цилиндрической стенки.

              Температурное поле:

Уравнение теплопроводности после первого интегрирования:

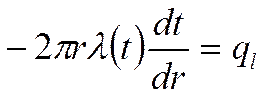
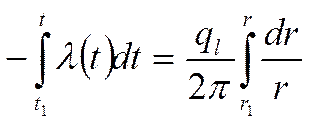
  Пусть 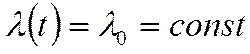 (не зависит от температуры)

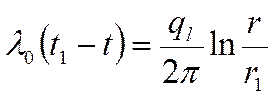
Подставляя в это выражение значение для q_l, получим:

 

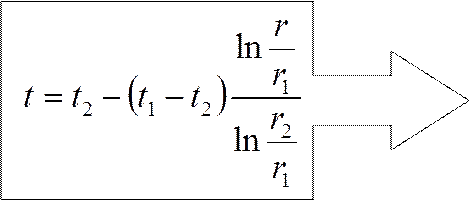температурное поле в                        однослойной стенке.

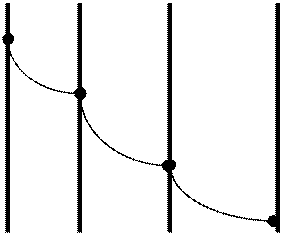
Так как плотность теплового потока уменьшается с увеличением радиуса, то кривая имеет следующий вид:

 

 t₁                                                                                                                             t₂

                      t₂

                                t₃

                                                                                t₁

                                            t₄

  Обоснование подобного вида кривой следует из понятия производной и касательной к графику функции. Из математики известно, что тангенс угла наклона касательной к графику функции в некоторой точке есть значение производной этой функции в данной точке. Из теории тепломассообмена

 

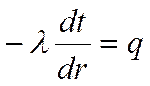известно, что:                    .

 

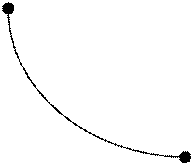
      tЕсли провести к этому графику множество                                     касательных, то при увеличении координаты r угол jуменьшается.

                                                           

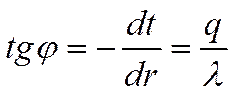
                  t₁                                                                                                                   

                                                                                                                             (*)

                                               t₂                     Как было сказано выше, поток тепла q

                                                rс увеличением радиуса r уменьшается.

                                   j   Если значение l не изменяется, то из

                                                                       выражения (*) следует что значение

                                                                    так же уменьшается.

Из графика видим, что уменьшение значения j а значит и          при увеличении r  возможно только при данном поведении кривой                                         (кривая вогнутая а не выпуклая).

  Какое температурное поле в i- том слое?

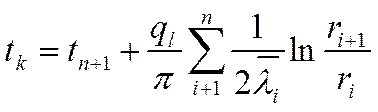
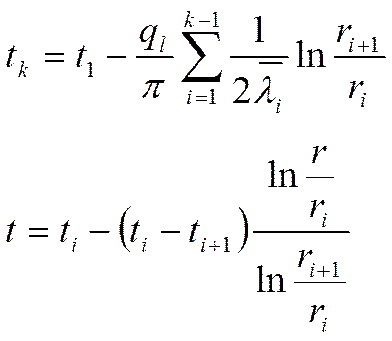Определим граничные значения температур:

Температурное поле и плотность теплового потока в шаровой (сферической) стенке.

 

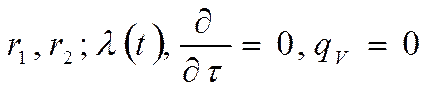Заданы:

                                  Так же заданы граничные условия первого рода: