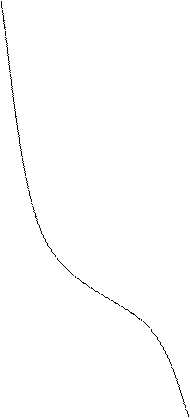
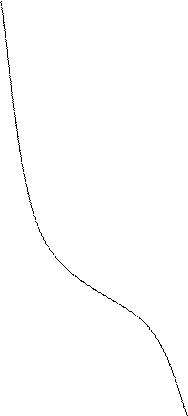
- характеристическое
уравнение для расчёта
корней ![]()
 |
|||||||||||||
 |
 |
||||||||||||

 правая
часть
правая
часть
левая
![]()
![]()
 часть
часть
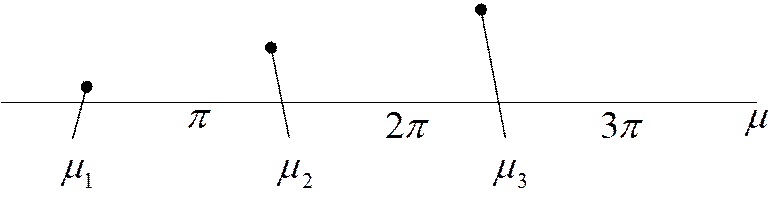 |
Решений этого характеристического уравнения бесконечное множество. Решению удовлетворяет множество принятых нами значений k.
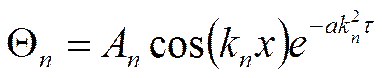
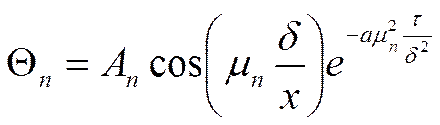
Введём
безразмерную координату: 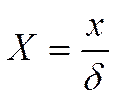
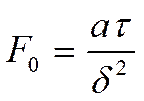 - критерий Фурье или безразмерное время.
- критерий Фурье или безразмерное время.
Общее решение задачи:
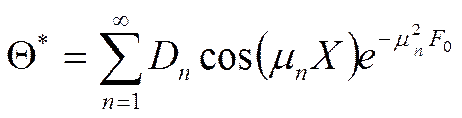
где:
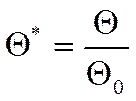 - безразмерное отношение
разности температур.
- безразмерное отношение
разности температур.
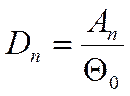
Согласно
принятому начальному условию ![]() :
:
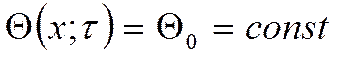
через коэффициент А:
![]()
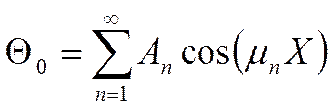 (*)
(*)
(это четная функция)
Если мы возьмём область
определения от ![]() до
до ![]() и
проинтегрируем от
и
проинтегрируем от ![]() до
до ![]() :
:
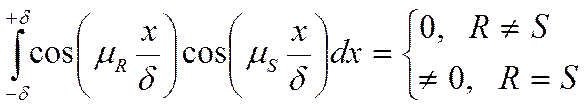
Домножим (*) на ![]() и
проинтегрируем:
и
проинтегрируем:
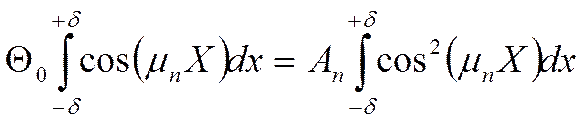
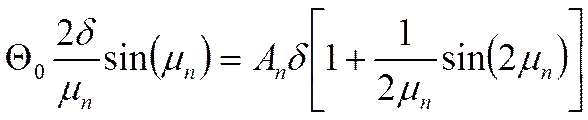
Константа Ап для любого частного решения определяется начальными условиями задачи:

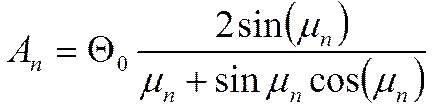
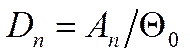
![]()
Анализ решения.
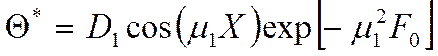
![]()
![]()
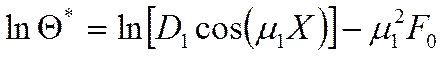
F(Bi) F(Bi,X)
Х=0 и на поверхности Х=1)
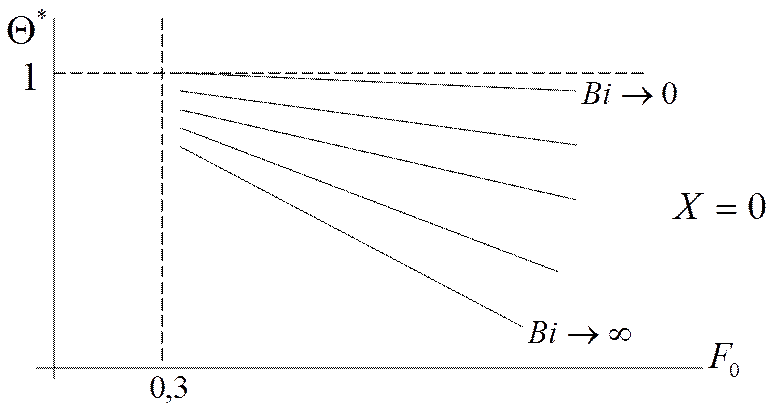 |
Одна монограмма для Х=0, другая – для Х=1
Случаи вырождения чисел БИО.
Вырождение – достижение некоторых предельных значений. Предельными значениями БИО являются бесконечно большие и бесконечно малые.
1)
Бесконечно большое числоBi: ![]() .
.
можно применять предельный подход:
при ![]() :
: 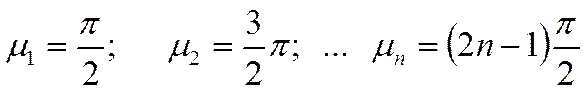
Если мы рассмотрим выражение
для ![]() :
:
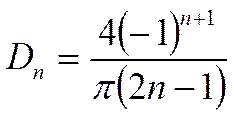 причём:
причём: 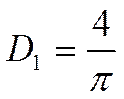
так
как 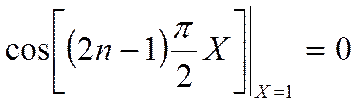 , то
, то 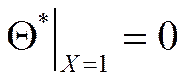
Изобразим это:
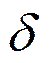 |
|||||
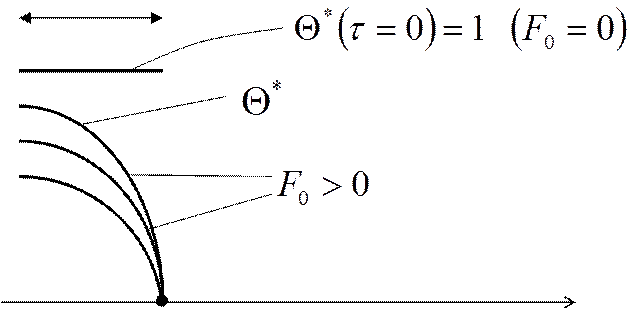 |
![]()
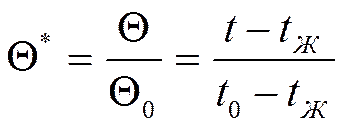
![]()
Если поместить пластину в печь, то температура на её поверхности сразу станет равной температуре печи.
Если 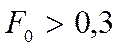 , мы получим:
, мы получим:
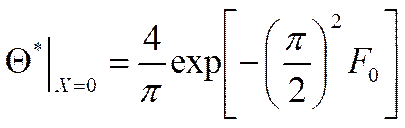 - температура на оси при больших временах.
- температура на оси при больших временах.
Выражая ![]() через
через 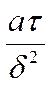 , мы
получим:
, мы
получим:
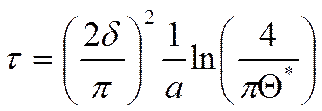
Это время достижения заданной температуры в центре пластины.
2)
Бесконечно малое Био: ![]()
На практике Био вырождено,
если ![]()
Корни характеристического уравнения:
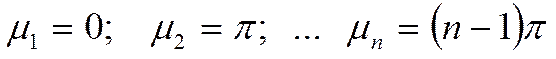
При этом: ![]()
Для тонких тел температура
описывается одним членом ряда независимо от числа ![]() .
.
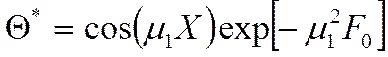
Определим порядок ![]() при
при ![]() :
:
![]()
![]()
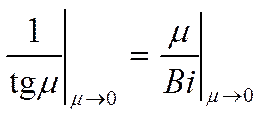
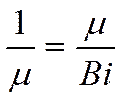

Поэтому для малых Био поле температур описывается одним единственным членом ряда:
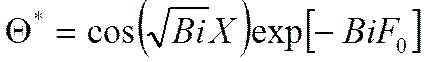
Изобразим эту зависимость:
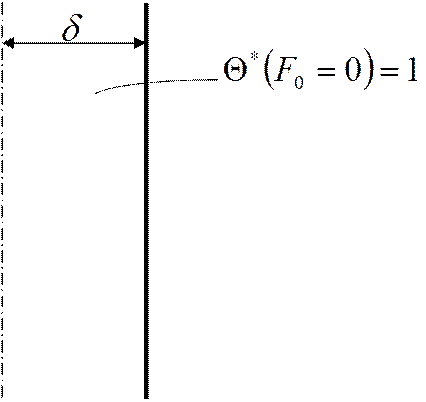 |
![]()
![]()
![]()
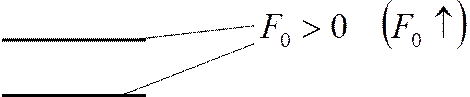 |
|||||
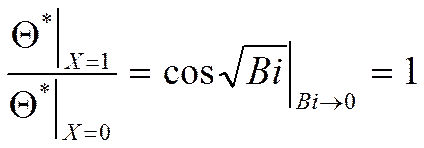
Это означает, что разница температур в центре и на поверхности стремится к нулю.
3)
Рассмотрим ![]() :
:
 |
|||||
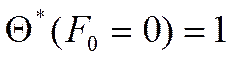 |
|||||
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.