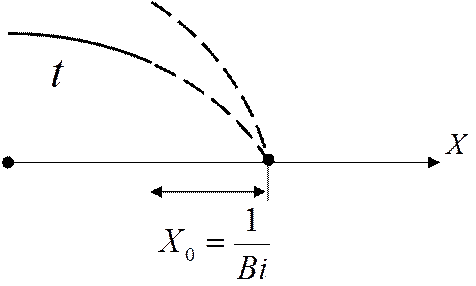Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 13

 

                                       

 

Охлаждение (нагревание) бесконечного цилиндра.

  Рассмотрим бесконечный цилиндр радиусом .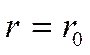

Известен материал, , . Цилиндр размещён в среде с постоянной , коэффициент теплоотдачи .

 

Начальная температура в любой точке цилиндра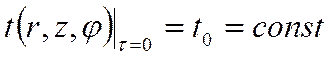

Задача является одномерной.

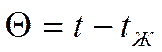
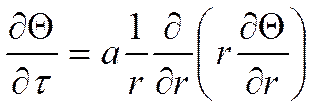
решением является: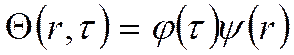

 

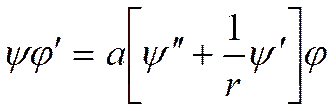
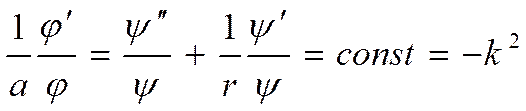
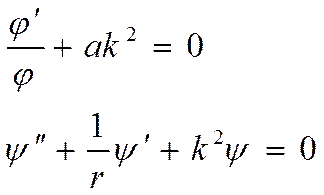
Почти уравнение Бесселя

  его решениями являются функции Бесселя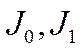

- функция Бесселя первого рода нулевого порядка;

- функция Бесселя первого рода первого порядка.

Начальные условия: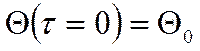

Граничные условия:

1) 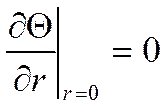              - условие симметрии.

2)            

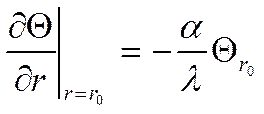
Общий вид решения:

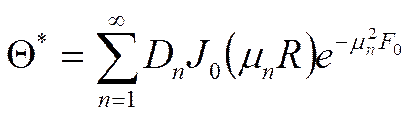
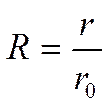        - безразмерный радиус.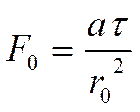   

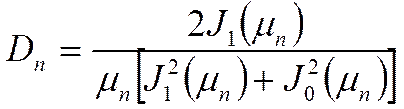
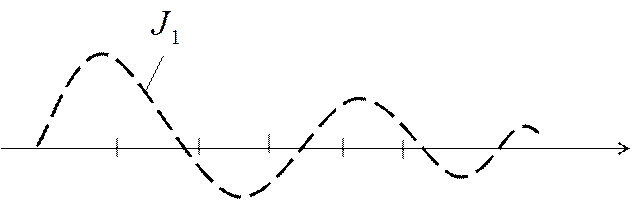
     J₀ – аналогично 

     J₁ – аналогично 

 

Функция       является производной 

     1                                                                            

 

                  2         4         6       8       10

-0,4

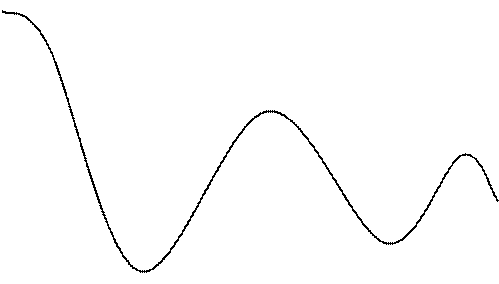
- бесконечные периодические функции с уменьшающейся амплитудой.

                                                                 (*)

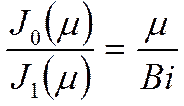Характеристическое уравнение для расчёта корней.

 

Анализ решения.

Поскольку временная функция такая же как и в предыдущей задаче для , температурное поле описывается так же одним членом ряда.

1) 

 

                                                                  

 

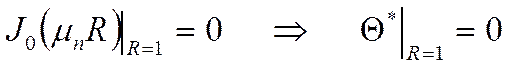
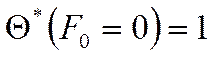
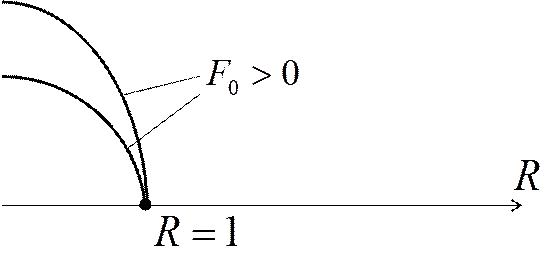Поверхностный слой цилиндра мгновенно принимает температуру окружающей среды.

2)                         

                                                                   (Порядок малости)

 

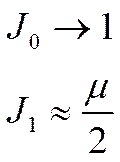
                                         подставим в (*), получим:

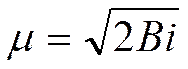
   Рассчитаем при :

   При  вне зависимости от Фурье решение описывается первым членом ряда:

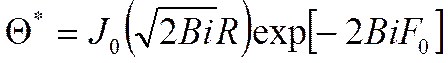
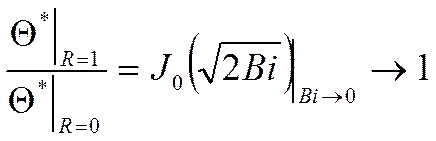
   Изобразим температурное поле при :

 

 

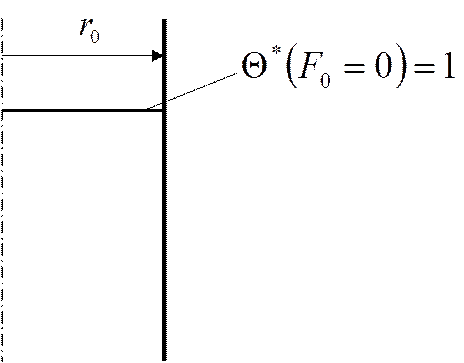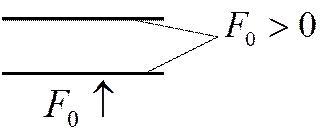            0                     1

 

Охлаждение (нагревание) тел конечных размеров.

Рассмотрим два варианта:

1)  Параллелепипед:

 

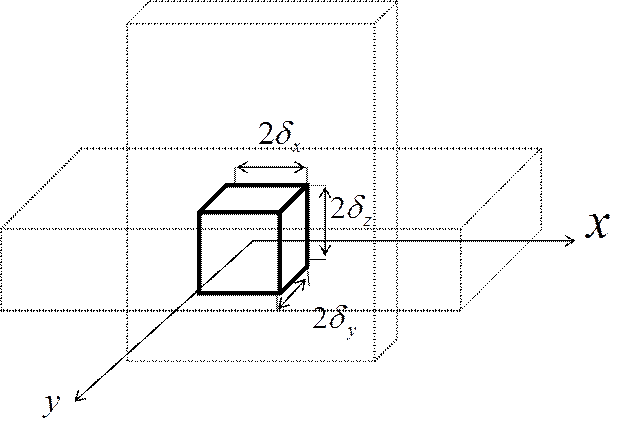  Разместим начало координат в центре параллелепипеда и обратим внимание на то, что параллелепипед есть пересечение трёх бесконечных пластин, лежащих в координатной плоскости.

  Теорема о перемножении решений: если безразмерная функция есть решение задачи для бесконечной пластины толщиной ,функция есть решение задачи для бесконечной пластины с толщиной , а функция  есть решение задачи для пластины толщиной , то общим решением задачи для параллелепипеда  будет функция равная произведению этих решений:

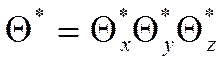
   Речь идёт о решении задачи с температурным полем.

Замечание:

·  Речь идёт только о безразмерных функциях.

·  Речь идёт об уравнении теплопроводности.

·  вид граничных условий должен быть одинаковым для трёх задач (условия III рода), а начальные условия должны быть равные и равны .

Если хотя бы одно условие не выполняется, то теорема не подходит.

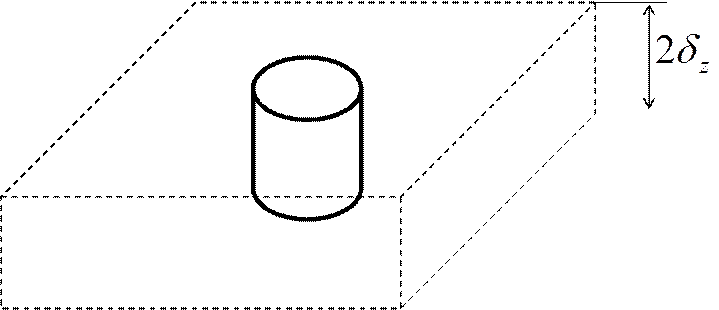
2)  Цилиндр конечных размеров:

                                   

                                                                                   Рассмотрим цилиндр - это

                                                                                пересечение двух бесконеч-

                                                                                ных тел – цилиндра и

                                                                                пластины.