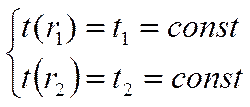 |
Здесь не существует торцевого эффекта, задача является одномерной:
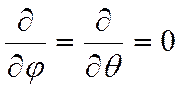
Уравнение теплопроводности для нашего случая:
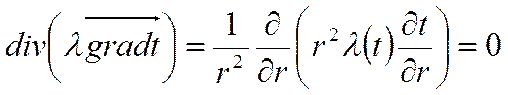
Проинтегрируем:
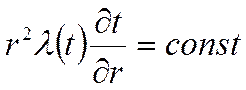
Рассмотрим два геометрических тела:
1) Шар – может выделять тепло, если есть внутренние источники тепла:
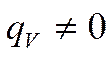
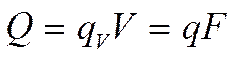
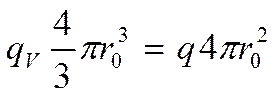
2) Шаровая (сферическая стенка)
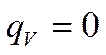

![]()
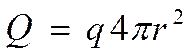 -
текущий радиус
-
текущий радиус
Домножим
на ![]() :
:
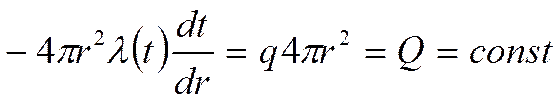 (*)
(*)
В сферической стенке, полня передаваемая (переносимая) энергия не зависит от радиуса и является величиной постоянной.
Умножим выражение (*) на 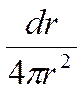 и проинтегрируем:
и проинтегрируем:
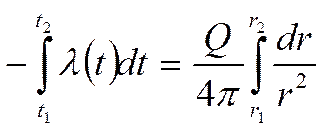 ;
умножим на
;
умножим на 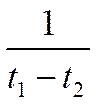
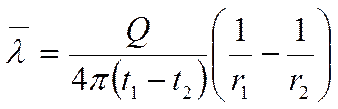

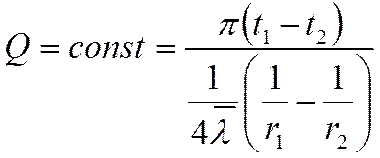
(*)
термическое сопротивление
шарового слоя.
Для многослойной сферической стенки:
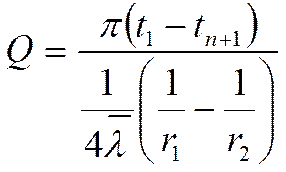
Температурное поле:
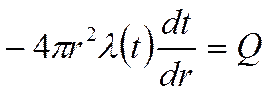
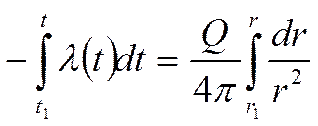
Рассмотрим простейший
вариант: пусть ![]()
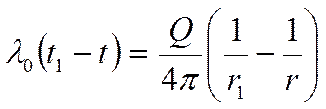

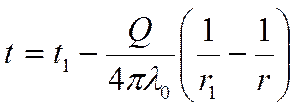 ; подставим значение для Q из выражения (*):
; подставим значение для Q из выражения (*):
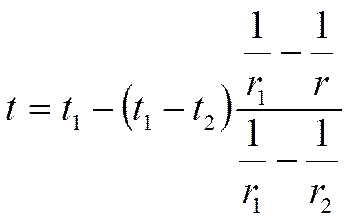
Это температурное поле для шарового слоя (гиперболическая функция).
Решение задач теплопроводности для граничных условий третьего рода.
Плоская стенка. Теплопередача.

![]()
![]()
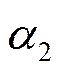
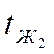
![]()
![]()
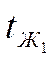
![]()
![]()
![]()
Заданы: 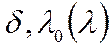
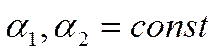 Значение коэффициентов теплоотдачи
Значение коэффициентов теплоотдачи
Среда представляется текучей
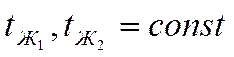 Кроме этого известно значение температур жидкости:
Кроме этого известно значение температур жидкости:
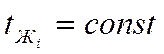 , отсюда
, отсюда 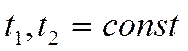
Граничные условия третьего рода заключаются в том, что нам известна плотность теплового потока:
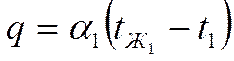 - граничные условия левой части стенки.
- граничные условия левой части стенки.
Рассмотрим связь между плотностью теплового потока и температурой стенки:
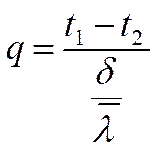
(см. решение ранее)
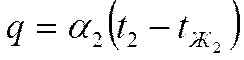 -
граничные условия для правой стенки.
-
граничные условия для правой стенки.
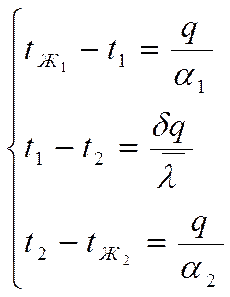 Переписывая наши выражения, получим:
Переписывая наши выражения, получим:
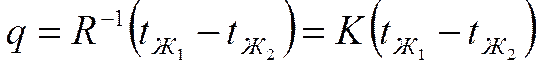 Сложив, получим:
Сложив, получим:
Мы получили выражения для плотности теплового потока при теплопередаче
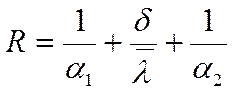 - термическое сопротивление теплопередаче
через плоскую стенку.
- термическое сопротивление теплопередаче
через плоскую стенку.
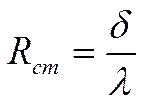
![]() - коэффициент теплопередачи через плоскую
стенку
- коэффициент теплопередачи через плоскую
стенку 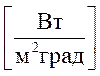
- термическое сопротивление материала плоской стенки.
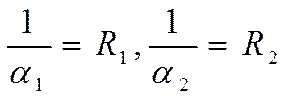 |
- термические сопротивления теплоотдаче.
Многослойная плоская стенка. Теплопередача.
Записывая выражение для разности температур между слоями и по гипотезе Ньютона -Рихмана, мы получим следующий результат:
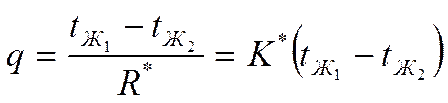
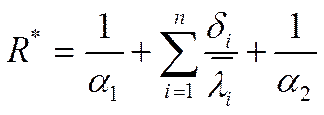 -
термическое сопротивление теплопередаче через многослойную плоскую стенку.
-
термическое сопротивление теплопередаче через многослойную плоскую стенку.
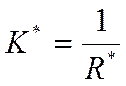 -
коэффициент теплопередачи через многослойную плоскую стенку.
-
коэффициент теплопередачи через многослойную плоскую стенку.
Цилиндрическая стенка. Теплопередача.
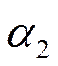 |
||||||||||
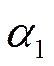 |
||||||||||
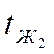 |
||||||||||



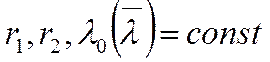 |
Заданы:
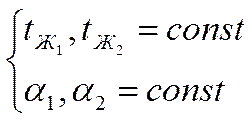
Нам известно, что :
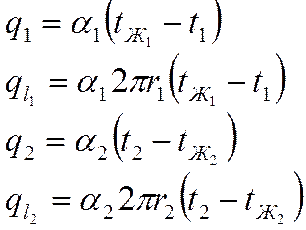
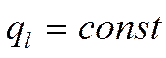
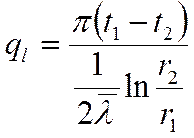 (см. решение ранее)
(см. решение ранее)
Переписывая наши выражения для разности температур и сложив их, получим:
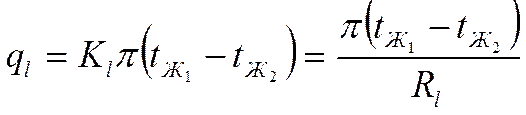
где: 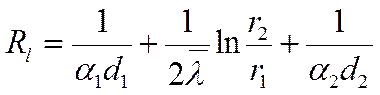 - термическое
сопротивление теплопередачи через цилиндрическую стенку
- термическое
сопротивление теплопередачи через цилиндрическую стенку 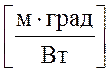
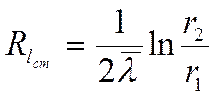 - термическое сопротивление
теплопроводности стенки.
- термическое сопротивление
теплопроводности стенки.
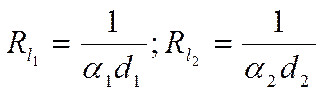
- линейное термическое сопротивление теплоотдаче через цилиндрическую стенку
Многослойная цилиндрическая стенка. Теплопередача.
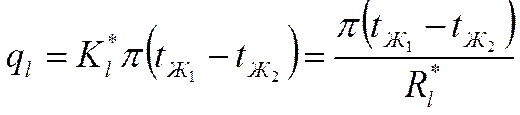
где: 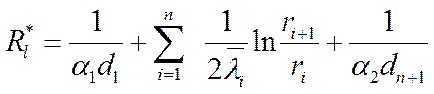 - линейное термическое сопротивление
теплопередаче для многослойной цилиндрической стенки.
- линейное термическое сопротивление
теплопередаче для многослойной цилиндрической стенки.
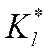 - линейный коэффициент теплопередачи через
многослойную цилиндрическую стенку.
- линейный коэффициент теплопередачи через
многослойную цилиндрическую стенку.
Запишем связь между плотностями теплового потока, учитывая что в цилиндрической стенке:
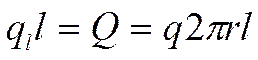
где
![]() - любой текущий радиус:
- любой текущий радиус:![]()
![]() - передаваемое через поверхность тепло.
- передаваемое через поверхность тепло.
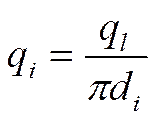 В нашем случае:
В нашем случае:
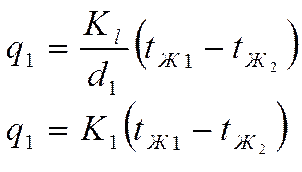 |
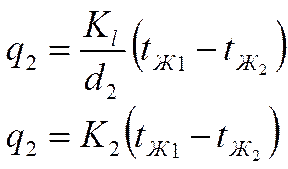 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.