Тепломассообмен. Теория тепломассообмена: Курс лекций, страница 4

                                                                                   По Стефану-

                                                                                   -Больцману

  Некоторые авторы выводят граничные  условия четвёртого рода (условие «сшивки»): если есть потоки субстанции, то на границе ни количество субстанции, ни её поток скачками меняться не могут. Граница является стоком, если такой скачок есть.

  Граничные условия третьего рода нельзя использовать, если неизвестен коэффициент теплоотдачи a . Он как правило сильнейшим образом зависит от температуры. В этом случае нужно использовать гипотезу Фурье:

 

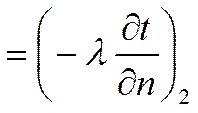
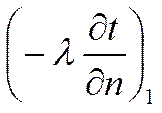
                                                                                               равенство

                                                                                               потоков

                                             ^{F                                              F}                     ;    

 

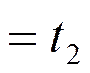                                                                          равенство энергий

F                      F(условие «сшивки»)

Задачи на граничные условия четвёртого рода называются сопряжёнными.

Геометрическая интерпретация граничных условий третьего рода.

 

                      жидкость       t          твёрдое тело        

            

                       F            B

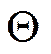
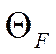
                           C                                     

                 t_ж          

                                  lA

                  nx

  Рассмотрим следующие точки: А,В,С.

;                                        ;   найдём l.

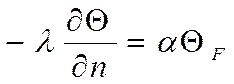Мы имеем: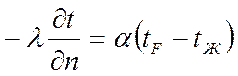

                                                                                                         (1)                                                           

                            

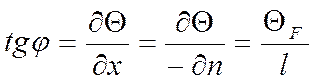
                                                                                                    (2)     

 

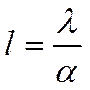
Сравнивая (1) и (2), мы получаем, что

 

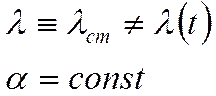
 Если                                                   то

  Любое изменение температурного поля в теле приводит к тому, что пересечение на границе не изменится (точка С)

Решение стационарных задач теплопроводности.

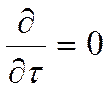
Температурное поле и тепловые потоки в плоской стенке

a)  Предполагаем, что внутренние источники (стоки) тепла отсутствуют:

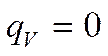
b)  Предполагаем, что стенка бесконечна по осям yи z.

         z                                      

                                                                   - постоянная толщина

                                                                              к плоскости стенки

                                   xt₁

        y

t₂

0                                                x

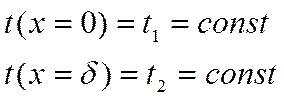Заданы граничные условия первого рода:

                                                                                        (по всей плоскости)

Искомые величины: t(x), q(x).

В бесконечной плоской стенке поле температур меняется в одном направлении – задача одномерная:

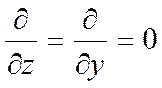
  Уравнение теплопроводности для нашего случая будет выглядеть следующим образом:

   (*)                                  

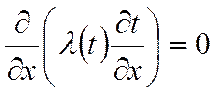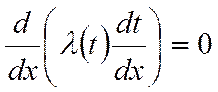
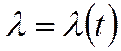
Проинтегрируем:

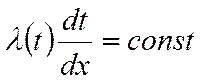
По Фурье:   

  В плоской бесконечной пластине (стенке) при граничных условиях первого рода в виде постоянных температур плотность теплового потока по нормали к стенке есть величина постоянная, независящая от координаты.

 Проинтегрируем (*) во второй раз:

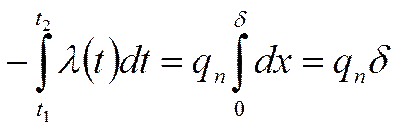
Разделим обе части уравнения на , получим:

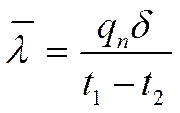
Где: 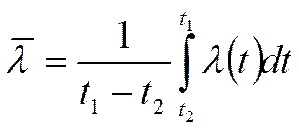  - среднее значение l для выбранного интервала температур.

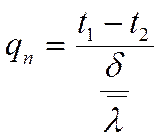    по аналогии: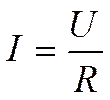   

Величина  есть термическое сопротивление плоского слоя.

Рассмотрим многослойную пластину, причём количество слоёв произвольно:

 

                                                                         Заданы:    ,