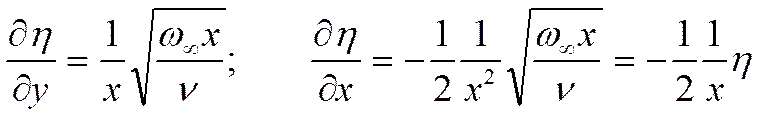
Определим безразмерную функцию потока:
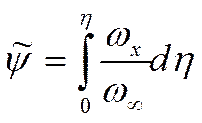
На стеночке ![]()
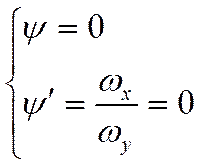
Сделаем замену переменных: 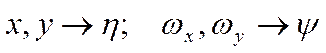 и преобразуем:
и преобразуем:
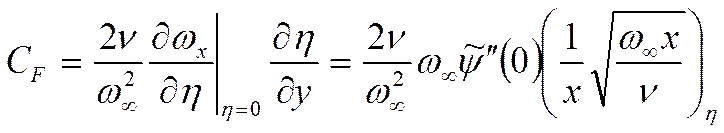
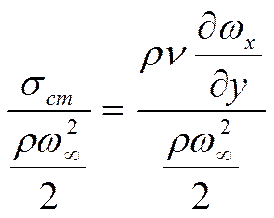
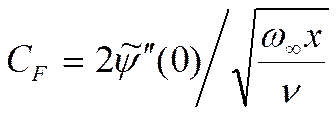
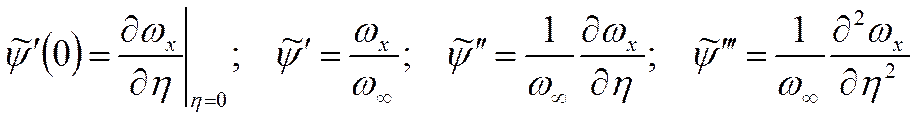
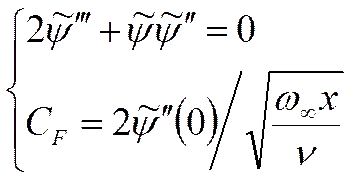 |
I- поле скоростей
II - коэффициент трения
Результатом
решения такой задачи будут: 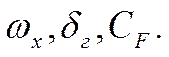
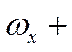 уравнение неразрывности
уравнение неразрывности 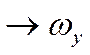 .
.
Для решений уравнений теплообмена достаточно уравнений I и II без их решения.
Запишем граничные условия:
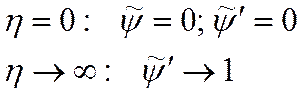
Система уравнений I,II – это математическая
постановка задачи для нахождения 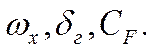 Эта
задача преобразуется в задачу Коши и решается численно.
Эта
задача преобразуется в задачу Коши и решается численно.
Результаты численного решения.

![]() - относительная величина пограничного
слоя.
- относительная величина пограничного
слоя.
![]() отличается
от
отличается
от 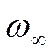 на 1%. Значение производной
на 1%. Значение производной ![]()
Выражение для коэффициента трения при ламинарном режиме течения у пластины:
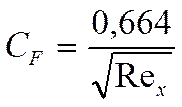
По профилю скорости:
 |


![]() 1
1
0,5
 |
1 2 3 4 5 6
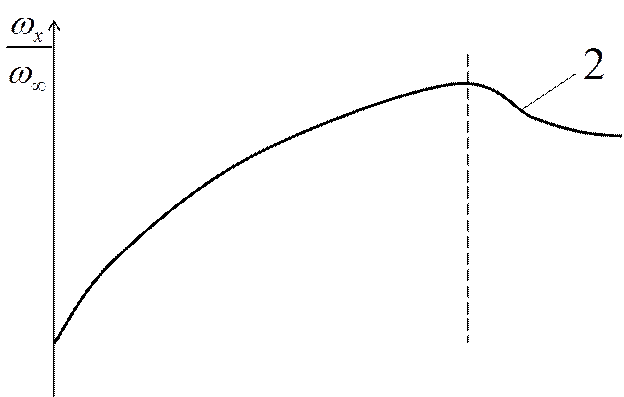
 |
1 – численное решение гидродинамической задачи;
2 – точное решение уравнения Навье-Стокса
Для точки ![]() :
:

 1
1
 |
![]() 0,5
0,5
1 2 3 4 5 6
1 – численное решение гидродинамической задачи;
2 – точное решение уравнения Навье-Стокса.
Из
этого следует, что решение гидродинамической задачи даёт качественно неверный
результат. Расхождение по поперечной составляющей сильно зависит от числа
Рейнольдса. Принято некорректным решать задачу для ![]() .
Решение гидродинамической задачи будет с погрешностью. Вывод: численный расчет
подтвердил наше предположение о то, что решение гидродинамической задачи с
погрешностью отличается от точного. Принято считать удовлетворительным решение
задачи при ламинарном течении при
.
Решение гидродинамической задачи будет с погрешностью. Вывод: численный расчет
подтвердил наше предположение о то, что решение гидродинамической задачи с
погрешностью отличается от точного. Принято считать удовлетворительным решение
задачи при ламинарном течении при ![]()
Решение задачи теплообмена на пластине.
Рассмотрим ту же самую задачу, но теперь пластина обогреваемая:
 |
|||
 |
|||
 |
|||
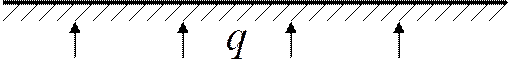 |
|||
Известно:
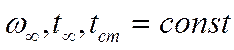 вдоль пластины.
вдоль пластины.
Введём:
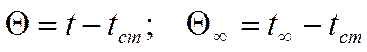
Введём
безразмерную 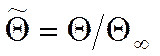
Математическая постановка задачи:
1)
Уравнение
энергии: 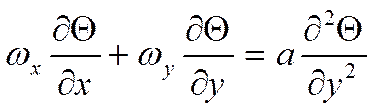
2)
Граничные
условия третьего рода: 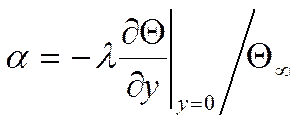
Граничные условия:
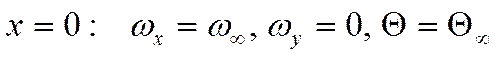
![]()
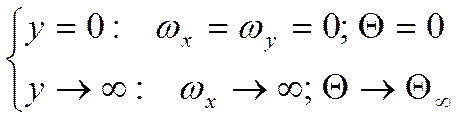
Заменим
![]() безразмерной
безразмерной ![]() , а координаты х и у – на
, а координаты х и у – на ![]() :
:
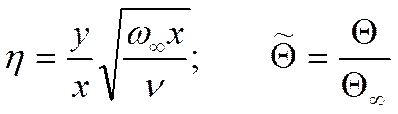
В качестве примера:
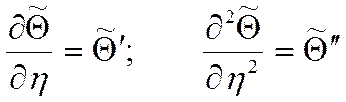
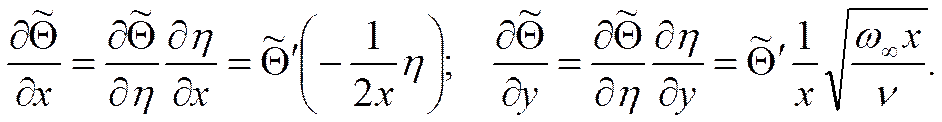
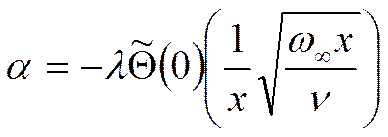
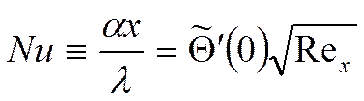
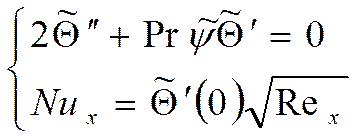 |
(1)
(2)
Это математическая постановка задачи теплообмена на пластине в безразмерной форме.
Граничные условия:
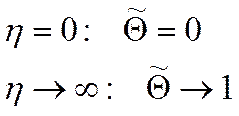
Выразим
![]() через уравнение I. Сделаем
предположение, что поле температур слабо влияет на поле скоростей, тогда мы
можем вернуться к решению гидродинамической задачи для необогреваемой пластины.
через уравнение I. Сделаем
предположение, что поле температур слабо влияет на поле скоростей, тогда мы
можем вернуться к решению гидродинамической задачи для необогреваемой пластины.
Из I следует: 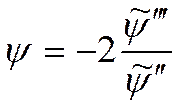 ,
подставим в уравнение (1):
,
подставим в уравнение (1):

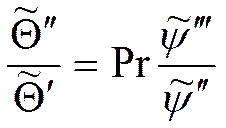

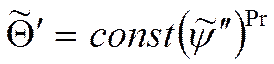
Используя граничные
условия, найдём значения ![]()
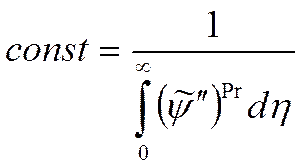
Решение имеет вид:
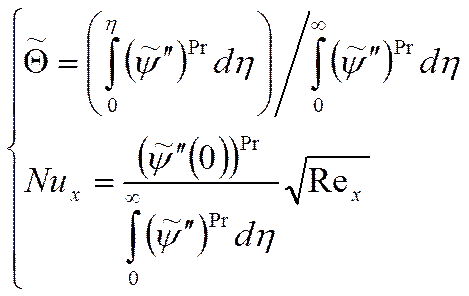
Мы решили задачу для интенсивности теплообмена
для пластины (распределение температур в пограничном слое). Аналитически задача
не решаема, если ![]() - не целое число, так как тогда
интеграл не существует. Рассмотрим задачу для значений числа Прандтля:
- не целое число, так как тогда
интеграл не существует. Рассмотрим задачу для значений числа Прандтля:
1) 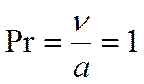
![]()
![]()
 Это
значит, что:
Это
значит, что: 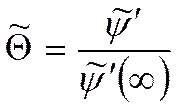
 |
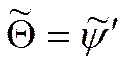
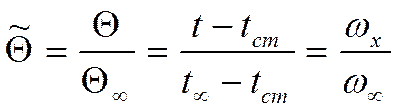
При
![]() безразмерное поле температур в ламинарном
пограничном слое совпадает с безразмерным полем температур.
безразмерное поле температур в ламинарном
пограничном слое совпадает с безразмерным полем температур.
Продемонстрируем это на графике:
 |
![]()
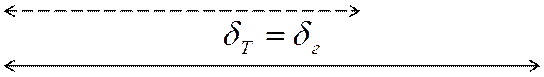 |
|||
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2)
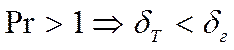
3)
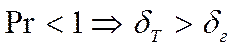
Режим течения ламинарный:
(*) 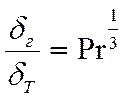 , если
, если ![]() (найдено опытным путём).
(найдено опытным путём).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.